Trap on the road to success
本記事の内容
はじめに
私はメーカーで製造データを用いた、設備の故障要因解析や、予知保全システムの開発を行っています。その中で感じた、統計解析上の「落とし穴」について記載します。解釈が間違っている部分も大いにあり得ますので、その点はご指摘いただけると有難いです🙇♂️
3行まとめ
- 4M視点でのデータを層別は大切！
- いわゆる「ビッグデータ」は実験計画に基づき取られたデータでないので、統計解析に難ありorz
- ランダム化、ランダムサンプリングされていないデータでの統計的仮説検定は意味をなさないので注意！ （やってしまいがちだけど、、）
製造データとは
ここで言う製造データとは以下とします。 製造データとは
具体的には、製品シリアルごと、もしくは特定サンプリングタイムごとの電圧、電流、圧力 等 の物理量（時系列データとして扱うことが多い）。現場のRDBに保存されていることが多い。
帳票への手書きやExcelで記録されることが多い
データレイクに保存されることが多い。
センサーデータ（クリックで拡大）
不良モードごとの発生個数・場所
外観検査画像
落とし穴3選
上記の中で、センサーデータを扱う上でぶち当たった落とし穴について説明します。
４M視点の欠如
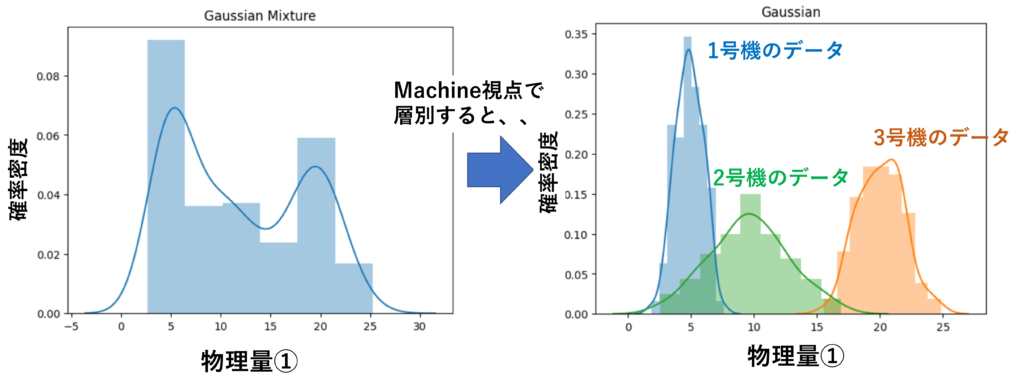
製造データの母数が変化し得る最大の要因が「4M」です。
4Mとは品質管理上の問題点を整理する際に使われる主要な視点になります。
4Mとは
初手は、これら4Mによってデータを層別した上で解析することをおススメします。
4Mの組み合わせをごちゃ混ぜにした状態で解析しても、目的とする変化点（例：品質異常が出る時特有のデータ変動）が見えないことが多々あります。
4M視点で層別すると見えてくる事実がある（クリックで拡大）
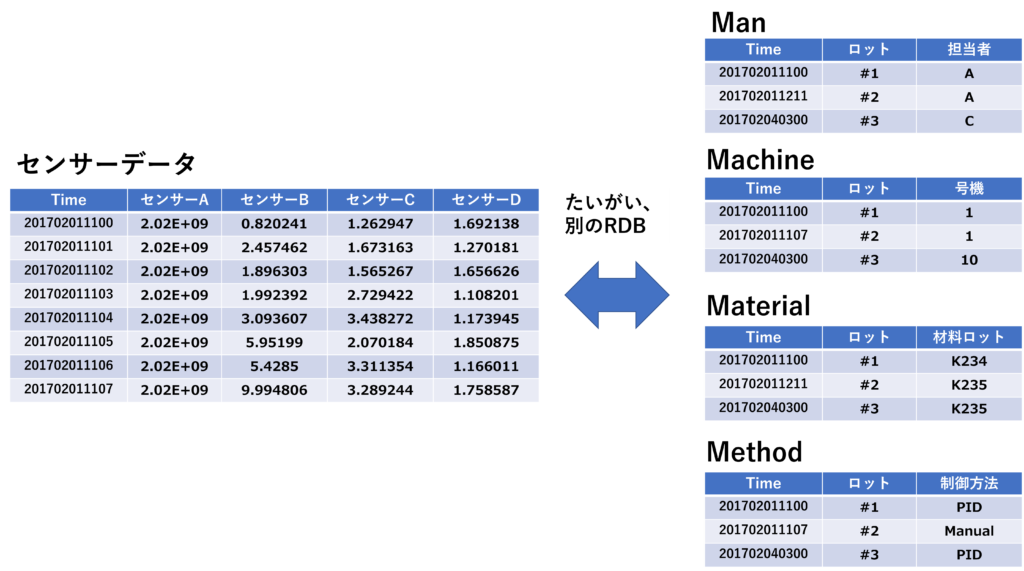
そして、やっかいなこととに、4Mデータとセンサーデータはたいがい同じRDBに入っていません💦（その現場のデータ基盤によりますが、、MESが入っていれば紐付いているのかな？）
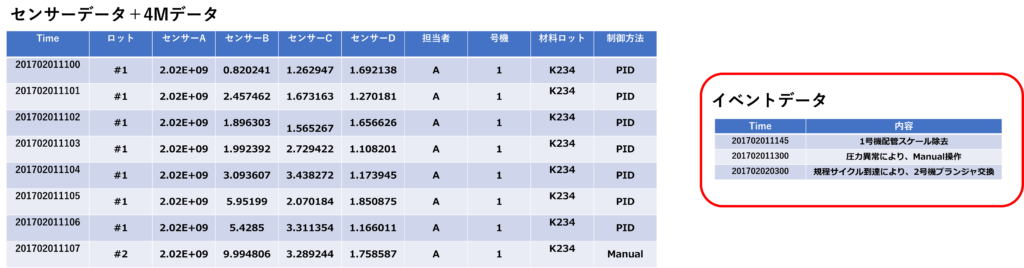
なので、データを紐付けた上で解析する必要があります。データ解析用途に作られたRDBでない場合は、致し方ないですね。 これらを紐付けた上で解析を行うことが定石になります。 さらに、保全記録に記録されているメンテナンス日時等「イベントデータ」も重要な情報になります。保全記録は紙であることが多く、扱いにくいです😅
センサーデータと4Mデータ（クリックで拡大）
センサーデータと4Mデータを連結します。イベントデータはテキストであることが多いため、整理して、解析時に参照できるように準備します。
センサーデータ＋4Mデータ（マージ済み）とイベントデータ
これらの準備をした上で解析を始めるようにしています。
対象が化学プラントの場合、PID制御、カスケード制御、モデル予測制御 等、制御方法が多々あり、組み立て加工よりもMethodの重要度が高いです。
余談ですが、過去、4M視点をすっ飛ばして、ディープラーニングにぶち込んだAIベンダーがいました。
案の定、何の結果も出ませんでした😅
4Mデータが無いとディープラーニングもお手上げ
ビッグデータのほとんどは実験計画法に基づきサンプリングされていない
製造業では、「ビッグデータ」というバズワードが流行っています。（私も役員報告等で使っています（笑）） 近年、大量のセンサーデータをPython等を使って簡単に・素早く扱える環境が整ってきました。 しかし、上記のデータを統計学で処理するには大きな問題があります。
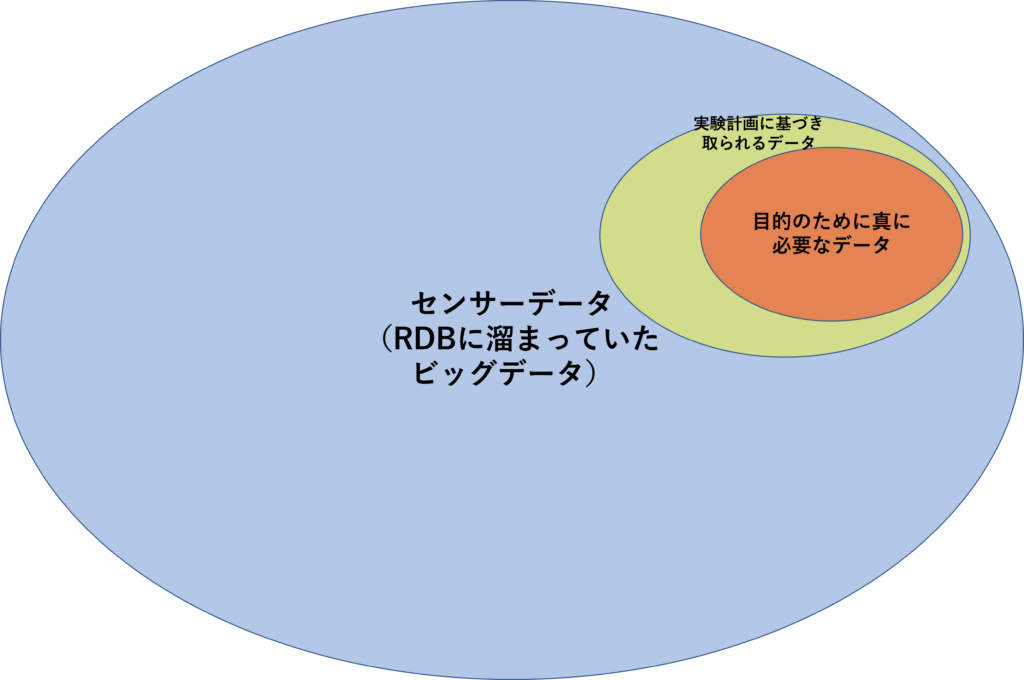
それは、実験計画法に基づき取られたものではないということです。 もっと言えば、データ解析目的で取っているデータでないことがほとんどです。本来、制御やメンテナンス目的に取っているデータであることが多いです。これが統計モデルを作成する際の大きな壁となっています。図にすると以下のようなイメージです。（A）の場合、勝ち筋がありますが、（B）の場合は詰みます。
（A)ラッキーな場合（クリックで拡大）
（B)詰む場合（クリックで拡大）
ランダム化やランダムサンプリングされていないデータでは仮説検定できない
上記（B)の場合を前提にどのような問題が起きるか、ケーススタディで考えてみます。 以下のようなニーズがあったとします。
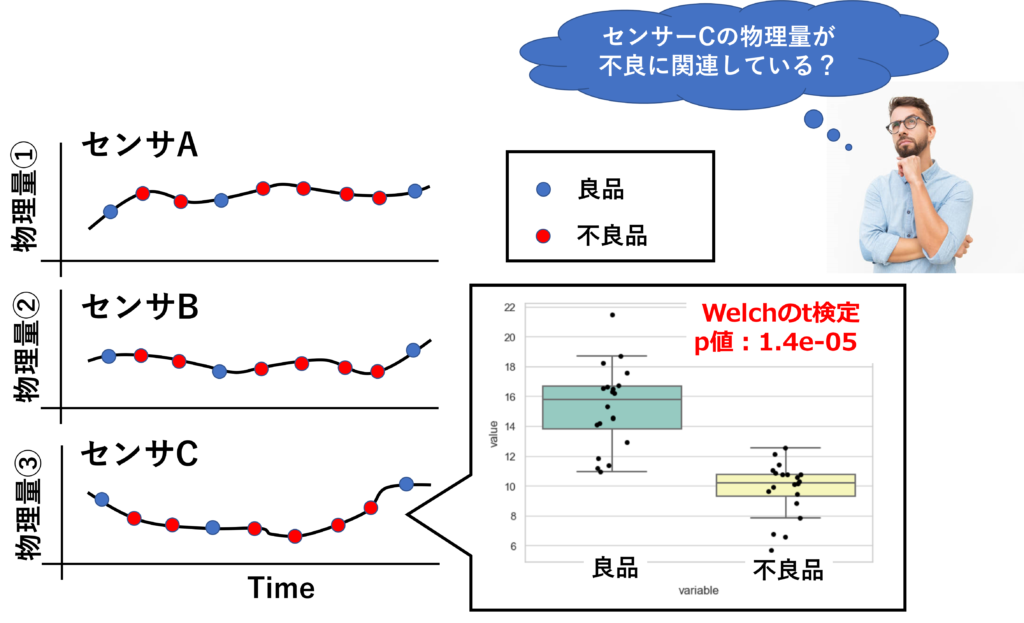
「不良品が発生した際に、特異に変動しているセンサーを特定して、要因解析のヒントにしたい」
そこで、良品と不良品時のデータでt検定し、平均値の差が有意なセンサーを絞り込むことにしました。
$H_{0}$：良品時の母平均 ＝ 不良時の母平均
$H_{1}$：良品時の母平均 ≠ 不良時の母平均
有意水準は両側5%とする。
t検定結果（クリックで拡大）
その結果、センサーCで測定している物理量③のみp値<0.05となりました。 この時、物理量③の平均値の差は統計的に有意と言えるでしょうか？
統計的に有意と言えない可能性が高いです。理由としては、物理量③が意図的にランダム化、およびランダムサンプリングされた値ではないからです。4Mデータが偏っている可能性があります。例えば、不良品のデータは特定号機からしかサンプリングされていない、とかよく起こり得ます。
（たまたま、ランダム化やランダムサンプリングになっている可能性もあるでしょうが、そんな幸運はまぁない）
統計モデルに必要な前提条件（下記動画20:00）
以下の動画が非常に勉強になりました。仮説検定の注意点が非常に分かり易く解説されています。
最後に
上の動画を見て「t検定1つを取っても、正しく使うのは容易でないな、、」と感じました。
勉強すればするほど、奥底が知れない統計学ですが、永い視点で取り組みたいと思います。
また、今回のような、手法の前提となる条件（意外に教科書に書いていなかったりする。当たり前すぎるからか？）を抑えて、正しく使えるよう精進していきたいです。
