以前、以下の記事でTimeGPTについて書きました。
今回は、続編として以下を書きます。
- TimeGPTの使い方
- TimeGPTとProphetの比較
Prophetを選んだのは、TimeGPTと同じくお手軽に時系列予測できるモデルの代表格だからです。
本記事の内容
TimeGPTが使える環境を用意する
TimeGPTはNixtlaという会社が運営しており、従量課金制のサブスクに登録することで使用できます。
上記ページ「Submit Interest」ボタンから必要事項を記載してAPI Keyを申請します。
申請が通れば、PythonのSDKを使って容易に時系列予測ができます。
SDKの使い方は以下のチュートリアルが参考になります。
ちなみに、MicrosoftがNixtlaへ出資しています。いずれ、TimeGPTはAzure Machine Lerarningに組み込まれるかもしれません。
https://twitter.com/nixtlainc/status/1722293248541208821?s=20
質問対応の特典
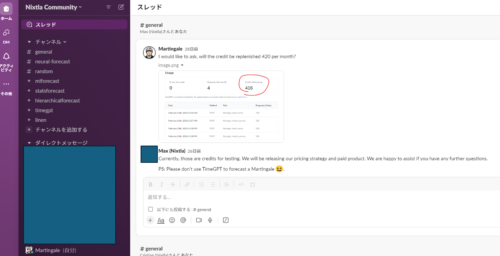
上記チュートリアルに記載無い内容（理論面、機微なチューニング方法）はSlackで開発者に質問できます。SlackはAPI Keyを申請すると招待メールが届きます。
Nixtla CommunityのSlack（クリックで拡大）
TimeGPTの使用料金
入力データ、出力データ、ファインチューニングに使用するデータのトークン量に応じて課金されます。
| 0~1M token | 1～10M token | ＞10M token | |
| Input | 0.0012 | 0.00012 | 0.00006 |
| Output | 0.0032 | 0.00032 | 0.00008 |
| Fine-Tune | 0.004 | 0.0008 | 0.0004 |
※単位は全て米ドル
初期使用時には$981の特典が付きます。なので、その範囲内であれば無料で使えます（2024/1月に申請した時の情報ですので、今もキャンペーン継続されているかは分かりません）。上記、価格はAPI Keyの申請が通った後、以下のページから確認できます。
使用料金には十分気を付けてください。
TimeGPTのメリット
再度おさらいしておきます。
実装に使われている原論文は以下です。
TimeGPTのメリット
事前学習された知識を活かし、追加の学習なしに未知の時系列に対してゼロショットで高精度な予測を行えます。
⇒ 異常時の時系列データが少ない製造業で重宝しそうです。
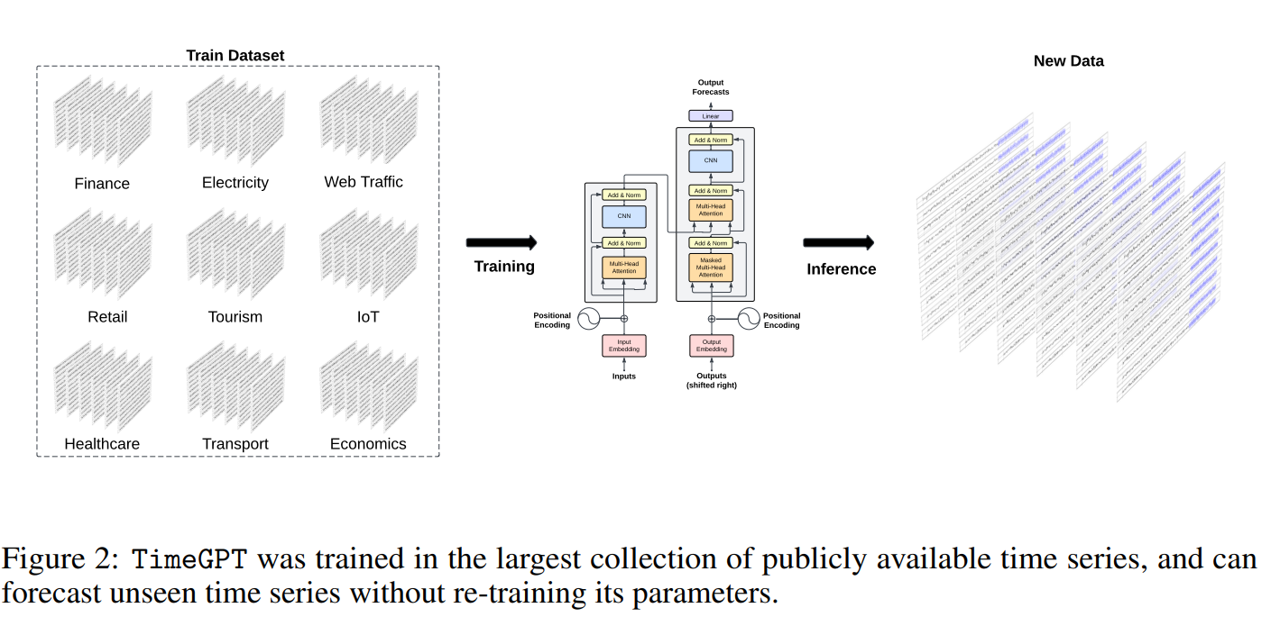
大規模で多様なデータセットでの事前学習 1000億ポイント以上の、様々な分野・特性の時系列データで事前学習されています。これにより、様々なタイプの時系列に対する汎用的な知識を身につけています。
⇒ タスクごとにモデルを作成し直さなくて良いので、運用コストを下げられます。
SDKからAPI Keyを読み込むコードを数行書くだけで予測可能です。
⇒ Python初心者にも優しい作りです。が、コーディングは必要です。
シンプルで高速な推論 単純な線形層による出力マッピングのため、推論が非常に高速です。⇒ 数百万点の予測が数秒で実施できるとのこと（実測していません）。
TimeGPTとProphetで電力使用量データの予測を行う
では、時系列データの予測を実施します。
データセット
以下の、1時間当たりの電力使用量のデータセットを使いました。
今回は12時間分のデータを予測します。
EDA
import pandas as pd
from nixtlats import TimeGPT
import os
from dotenv import load_dotenv
load_dotenv()
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from prophet import Prophet
from sklearn.metrics import mean_squared_error, mean_absolute_error
plt.style.use('fivethirtyeight') # For plots
# 訓練データの読み込み
## Datetime列をdatime型で読み込み
pjme_df = pd.read_csv(r'../data/AEP_hourly.csv', parse_dates=["Datetime"])
print(pjme_df)
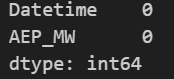
#欠損の有無を調べる
print(pjme_df.isnull().sum())
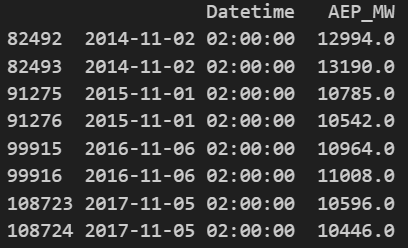
# Datetime列に重複したデータがあるか確認
print(pjme_df[pjme_df.duplicated(subset='Datetime',keep=False)])
# Datetime列の重複したデータを削除する
pjme_df = pjme_df.drop_duplicates(subset='Datetime')
# "Datetime" 列でソート
pjme_df = pjme_df.sort_values('Datetime')
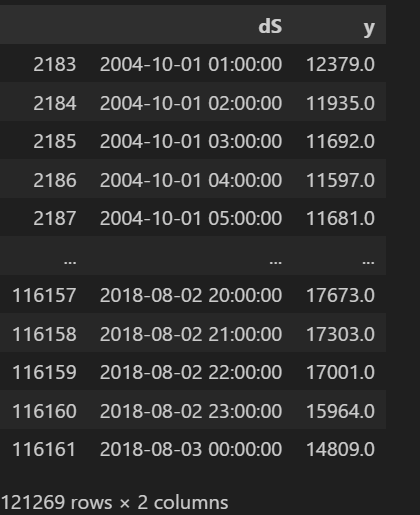
# Prophetの仕様に合わせて列名を変更
pjme_df = pjme_df.rename(columns={'Datetime': 'dS', 'AEP_MW': 'y'})
print(pjme_df)
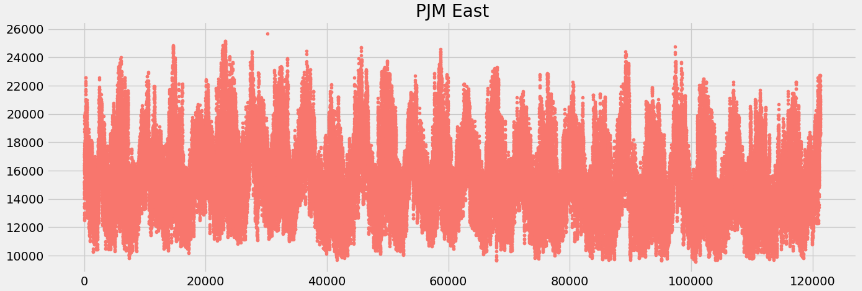
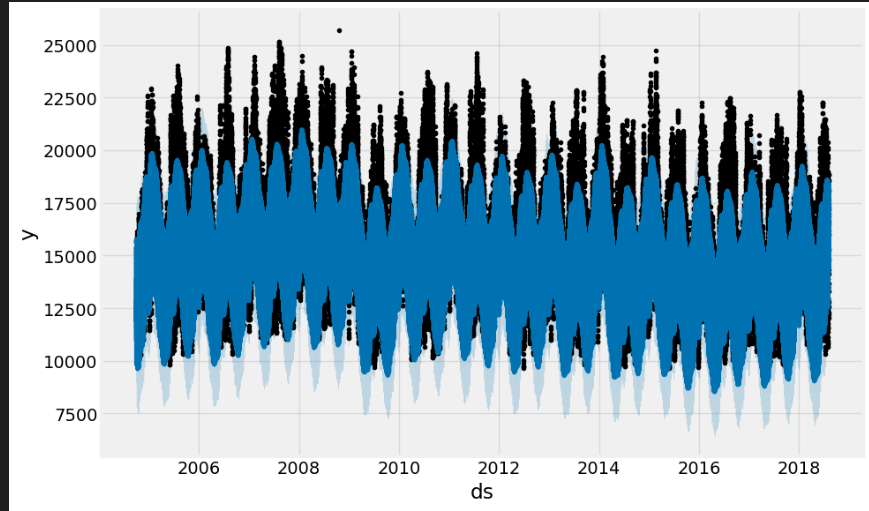
# 全期間にわたる電力量（y）の可視化
color_pal = ["#F8766D", "#D39200", "#93AA00",
"#00BA38", "#00C19F", "#00B9E3",
"#619CFF", "#DB72FB"]
pjme_df.y.plot(style='.', figsize=(15,5), color=color_pal[0], title='PJM East')
plt.show()
全期間の電力使用量データ（クリックで拡大）
Prophetによる予測
m = Prophet()
m.fit(pjme_df)
future = m.make_future_dataframe(periods=12, freq='H')
print(future)
# 予測の実行
forecast = m.predict(future)
# 予測結果の可視化
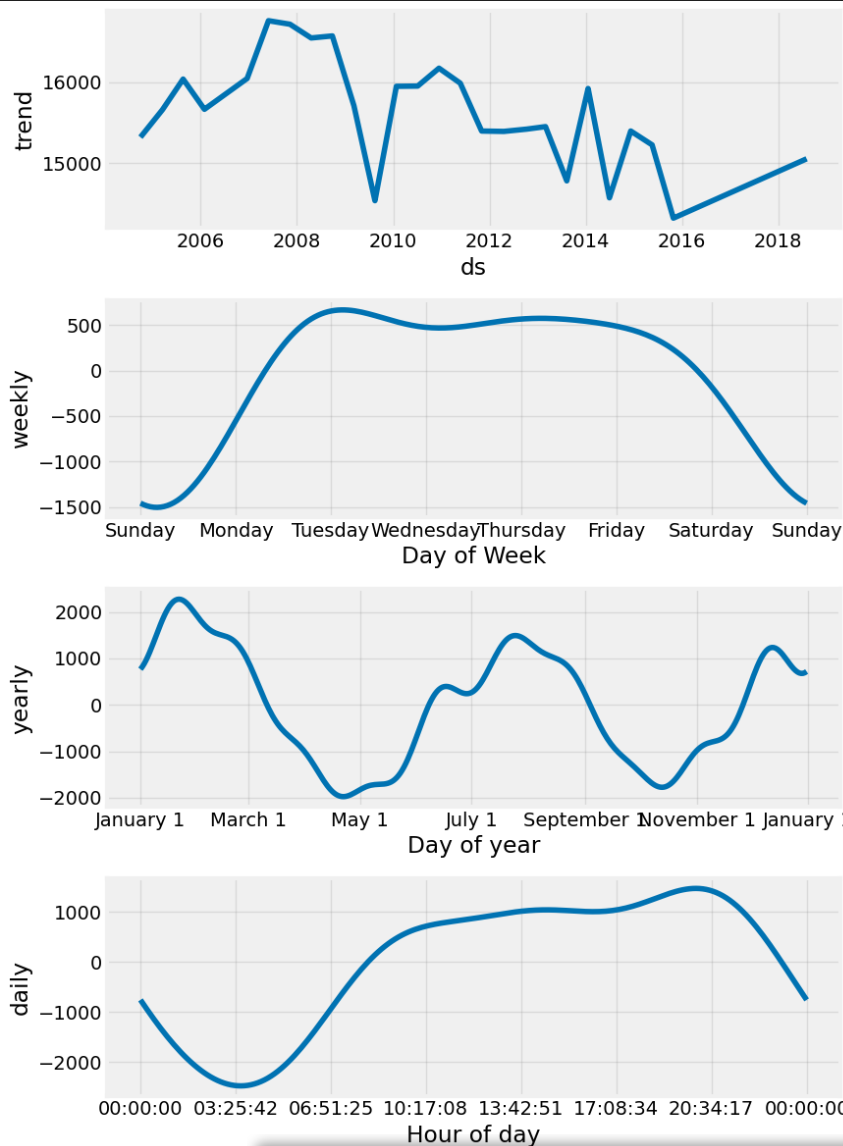
fig1 = m.plot(forecast)
fig2 = m.plot_components(forecast)
Prophetによる予測（黒：実測、青：フィッティング＋予測、薄青：80%信頼区間）（クリックで拡大）
各種トレンド（クリックで拡大）
予測区間付近を拡大した図が以下です。
以下では、timegptモジュールは可視化のためだけに使用しています。
# forecastの列名を変更
forecast = forecast.rename(columns={'yhat_lower':'yhat-lo-80', 'yhat_upper': 'yhat-hi-80'})
timegpt.plot(pjme_df[-50:],
forecast[["ds", "yhat",'yhat-lo-80', 'yhat-hi-80']][-62:],
time_col='ds', target_col='y',
level=[80]
)
Prophetのフィッティング＋予測 ※紺：実測、ピンク：フィッティング＋予測、薄ピンク：80%信頼区間（クリックで拡大）
TimeGPTによる予測
# インスタンス化
timegpt = TimeGPT()
# 予測実行
timegpt_fcst_df = timegpt.forecast(
df=pjme_df, h=12, freq='h', level=[80, 90],
time_col='ds', target_col='y',
add_history=True,)
予測区間付近を拡大した図が以下です。
以下では、timegptモジュールは可視化のためだけに使用しています。
timegpt.plot(pjme_df[-50:],
timegpt_fcst_df[-62:],
time_col='ds', target_col='y',
level=[80, 90])
TimeGPTのフィッティング＋予測 ※紺：実測、ピンク：フィッティング＋予測、薄ピンク：80%信頼区間と90%信頼区間（クリックで拡大）
TimeGPTとProphetを比較
初めにお断りさせていただきます。
上記まで実施したところで、従量課金が予算オーバーになってしまったため詳細の検証ができていません。また、予測したデータをpickle等で保存し忘れたため、RMSEを比較するなどの定量的な比較ができていません(;^_^A
また、グラフの縦軸を揃える前にTimeGPTが使えなくなってしまいました。下記グラフの縦軸が異なることに注意ください。
以下では定性的な比較を行います。ProphetとTimeGPTの結果を再度並べて比較します。
ProphetとTimeGPTの比較（クリックで拡大）
季節性へのフィッティングの差
Prophetは、TimeGPTに比べて24H周期の変動を上手く捉えられています。
以下がProphetのモデル式です。
Prophetのモデル式（クリックで拡大）
※出典は以下の論文です。
$s(t)$が周期成分になります。
具体的に書くと以下になります。
$s(t)=\sum_{n=1}^N(a_{n}cos(\frac{2πnt}{P})+b_{n}sin(\frac{2πnt}{P}))$
$P$は成分に応じた周期です。年周期なら$365.25$、1週間周期なら$7$、1日周期なら$1$です。
最適な$N$とパラメータ（$a_{1},,,,a_{n},b_{1},,,,b_{n}$）、をAIC基準で決めます。
周期的な任意の関数が三角関数の和で表される「フーリエ級数展開」の考え方を採用しています。
例えば$N=10、P=1$の場合、$s(t)$は以下の様に表せます。
$s(t)=a_{1}cos(2πt)+b_{1}sin(2πt)+・・・+$
$a_{10}cos(20πt)+b_{10}sin(20πt)$
$=X(t)β$
ここで、$X(t)=[cos(2πt), sin(2πt), ・・・,$
$cos(20πt), sin(20πt)]$
$β=[a_{1},b_{1},・・・,a_{10},b_{10}]$です。
これらを踏まえると、$s(t)=X(t)β$と整理できます。たたし、$β$の事前分布はスムージングのために$Normal(0,σ^2)$を仮定しています。
この様に式を整理するのは、パラメータを推定し易いという解析上の理由だと思います。
今回用いた電力使用量のデータは、明らかな周期性がありました。モデルに明示的に季節成分を組み込んだProphetが上手くフィッティングできているのはそれが理由だと思います。
一方、TimeGPTはTransformerベースの時系列モデルで、[Vaswani et al., 2017]に基づく自己注意機構を採用しています。TimeGPTは過去の値の窓を取り、局所的な位置エンコーディングを追加して入力を強化し、予測を生成します。
TimeGPTのモデル概要（クリックで拡大）
予測タスクの目的は以下の条件付き分布を推定することです。
$P(y[t+1:t+h] | y[0:t] , x[0:t+h]) = $
$f_{θ}(y[0:t] , x[0:t+h])$
時間毎の時系列データセットに対しては、予測ホライズン$h$=24と設定されます。
TimeGPTの学習では、過去のデータポイントを基に次のデータポイントを予測する自己回帰的なアプローチを取ります。このアプローチは、長期間の依存関係や複雑なパターンを捉えるのに有効ですが、明示的な季節性のモデリングの視点が欠けています。Transformerモデルは非線形関係を捉える能力に優れていますが、季節性のような周期的なパターンを直接的にモデル化するメカニズムは持っていません。
Prophetは周期性を直接的にモデル化するのに対し、TimeGPTはその構造上、季節性を暗黙的にしか捉えられません。季節性のような定期的なパターンを捉えるためには、周期を明示的にモデルに組み込むことが重要です。TimeGPTは長期間の依存関係や複雑なパターンの捉えることには優れていますが、季節性を含む周期的なパターンの捉え方には限界があるため、Prophetに比べて季節成分を上手く捉えられないという現象が生じたと思われます。
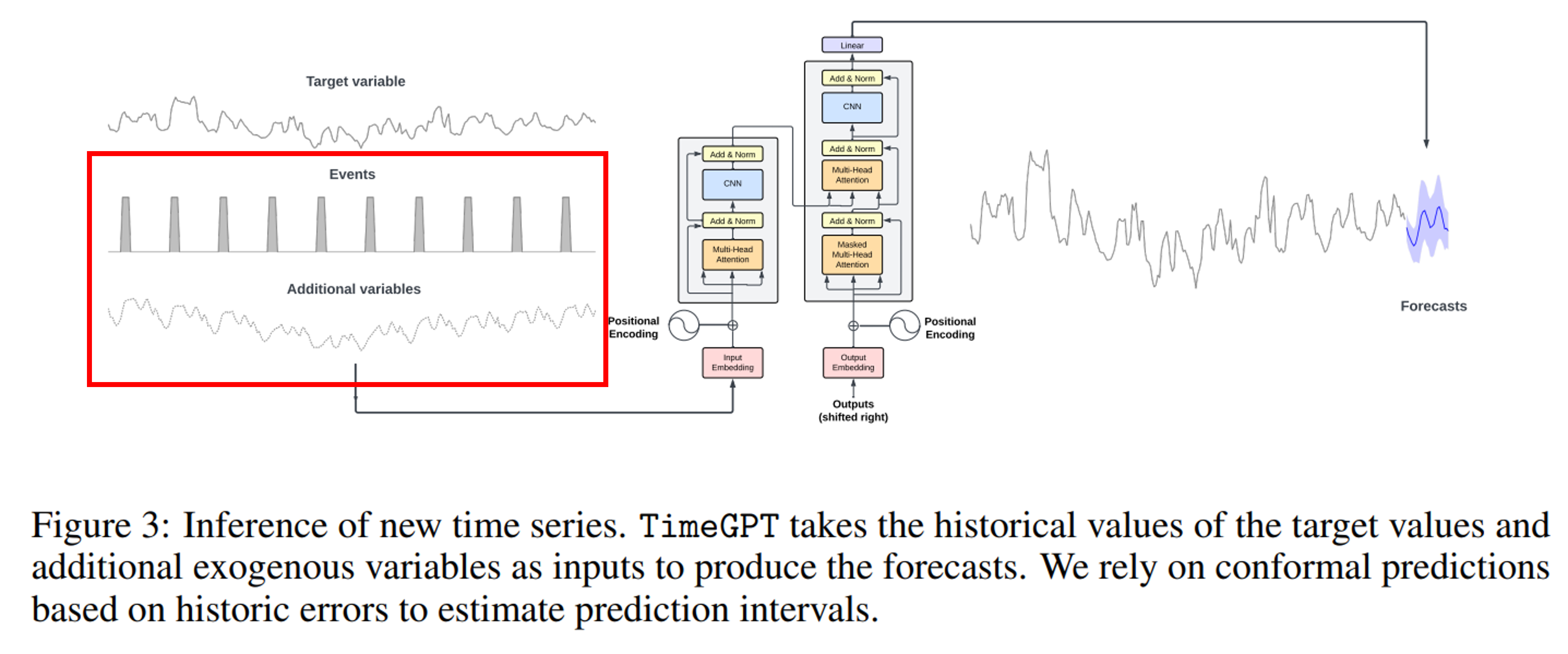
外生変数も追加できる
TimeGPTは目的変数だけでなく、外生変数を追加して予測精度を高められる機能を備えています。
今回のデータの例だと、当該地域の天候や気温を入れてみると面白いかもしれません。外生変数の導入方法も上記チュートリアルに載っています。
赤枠内が外生変数（クリックで拡大）
最後に
周期性のある時系列データの予測に関しては、Prophetの方が使い易いと感じました。
少なくとも、スケーリング則頼みで「はい、良しなに予測行ってこい！」では（古典的な手法である）フーリエ変換にも勝て無さそうな気がしました。
資金ができたら、以下を検証してみようと思います。
- $RMSE$等を使った定量比較
- TimeGPTをファインチューニングした上で比較
- （明確な）周期性のないデータでの比較
後日談
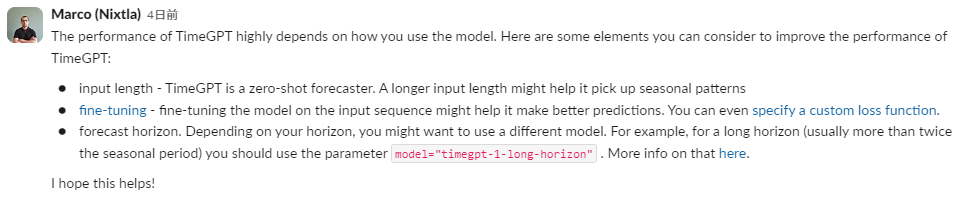
Nixtla内部の人から、TimeGPTでうまく周期成分を捉えるためのアドバイスを貰いました。有難い🙇♂️
クリックで拡大
TimeGPTのパフォーマンスは、モデルの使い方によって大きく変わります。
以下は、TimeGPTのパフォーマンスを向上させるために考慮できるいくつかの要素です。
- 入力の長さ - TimeGPTはゼロショット予測です。入力の長さを長くすれば、季節的なパターンを拾いやすくなるかもしれません。
- ファインチューニング - 入力シーケンスでモデルを微調整することで、より良い予測ができるかもしれません。損失関数をカスタム指定することもできます。
- 予測ホライズン - ホライズンによっては、異なるモデルを使うべきかもしれません。例えば、長いホライズン（通常は季節周期の2倍以上）には、model="timegpt-1-long-horizon" というパラメータを使うべきです。詳しくはこちらをご覧ください。
お役に立てれば幸いです！
