
はじめに
世界を危機に陥れてるCOVID-19ですが、
昨今勉強を進めている時系列分析で何か知見が得られないか調べてみることにしました。
しかしながら、初学者であるため間違った解釈をしている可能性があります。
どしどし、ご指摘お願いいたしますm(_ _)m
やりたいこと
VARモデル を使って中国の感染者数から韓国、日本への感染者数に対してグレンジャー因果性があるかを検定する。検定には、Pythonのstatsmodelsを使いました。

https://www.statsmodels.org/dev/index.html
VARモデル
ARモデル(自己回帰モデル)を多変量に拡張したものであり、以下の式で表されます。

Varモデルの優れている点は、自身の過去のデータだけでなく関係ありそうな他変数の過去のデータも回帰に使えることです。
例えば、仮に中国、韓国、日本の感染者数にそれぞれ相関があると仮定します。
その場合、1式は以下のように書き下せます。



沖本本pp.74によると
「モデルに含める変数は分析者の興味によって決めるものであり、目的に応じて様々です。
例えば、国際株式市場の関係を分析したい場合は、日本、アメリカ、イギリスの株式収益率などからなるベクトルを考えます。(中略)
重要なことは、分析者が、動学的関係に興味のある変数を全てモデルに含めることであるが、(中略)」
と書かれており、どんな変数をベクトルに加えるかは分析者の主観によるところもあるようです。
また、Varモデルで気を付けないといけないことは、非定常なデータには適用できないということです。
例えば、Pythonで時系列分析を扱う際によく用いられるstatesmodelsのVarモデルのページには以下の注意書きがあります。
非定常過程やトレンドを持つ過程は定常過程に変換してからVarモデルを適用しないと、不適切な結果を招くと書かれています。

Varモデルの解説はこちらのサイトが分かり易かったです。

https://tjo.hatenablog.com/entry/2013/07/30/191853
グレンジャー因果性
背後に明確な理論(経済・ファイナンス理論など)を仮定せずとも時系列データだけから因果性の有無を判断できる指標です。
沖本本pp.80には以下のように定義されています。

例えば、日本の感染者数から中国の感染者数へのグレンジャー因果性が存在しないということは、
2-A式に於いて、
$$A_{13}=A_{23}=・・・=A_{p3}=0$$
と同意になります。
つまり、中国の感染者数を表す式に於いて日本の感染者数に関する係数が全て0になるということです。
これは、以下の手順で判断できます。

グレンジャー因果性検定に於いて、
帰無仮説は「各変数群がその他の変数へ対してグレンジャー因果性がない」
になります。つまり、帰無仮説が棄却されればグレンジャー因果性があると判断されるわけです。
(2)の「制約を課した」という意味は、
2-A式に於いて、
$$A_{12}=A_{22}=・・・=A_{p2}=0$$
や
$$A_{13}=A_{23}=・・・=A_{p3}=0$$
を課すという意味です。
つまり、t時点の中国の感染者数をt-1〜t-p時点の中国の感染者数だけで表すと言うことです。
日本、韓国の過去の感染者数を考慮したモデルでの残渣
$$SSR_{1}$$
に対して、制約を課したモデル(中国の過去の感染者数だけを考慮したモデル)での残渣
$$SSR_{0}$$
が十分に大きければ中国の感染者数と日本、韓国の感染者数に因果性があると判断するわけです。
グレンジャー因果性には長短・短所があり、まとめると以下のようになります。
長所
●定義が非常に明確である
●時系列データを用いて容易に検定できる
短所
●因果性が存在する必要条件であるが、十分条件でない
●真の因果性の方向とグレンジャー因果性の方向が一致するとは限らない
●定性的概念であり、関係の強さが測れない
因果関係の方向がはっきりしている場合を除いては、ある変数が他の変数の予測に有用かどうかと言う観点で解釈するのが良いみたいです。
データを確認する
各国の感染者数のデータは以下のサイトからcsvで入手しました。
https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases
# 必要なライブラリのインポート
import statsmodels as sm
import statsmodels.api as sap
from statsmodels.graphics import tsaplots
from statsmodels.tsa import stattools
from statsmodels.tsa.api import VAR, DynamicVAR
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
sns.set()
# データの読み込み
Confirmed_df = pd.read_csv("time_series-ncov-Confirmed0122-0321.csv",\
header=1,index_col="#date", parse_dates=True)
##affected+infected+value+num(感染者数)をint型にキャストしておく
Confirmed_df["#affected+infected+value+num"] = Confirmed_df["#affected+infected+value+num"].astype(int)
# 国ごとにデータを取得する
# 日付け(昇順)でソートしておく
China_pre_cumsum = Confirmed_df[Confirmed_df["#country+name"] == "China"].sort_index()
US_pre_cumsum = Confirmed_df[Confirmed_df["#country+name"] == "US"].sort_index()
Italy_cumsum = Confirmed_df[Confirmed_df["#country+name"] == "Italy"].sort_index()
Spain_cumsum = Confirmed_df[Confirmed_df["#country+name"] == "Spain"].sort_index()
Germany_cumsum = Confirmed_df[Confirmed_df["#country+name"] == "Germany"].sort_index()
Korea_cumsum = Confirmed_df[Confirmed_df["#country+name"] == "Korea, South"].sort_index()
Japan_cumsum = Confirmed_df[Confirmed_df["#country+name"] == "Japan"].sort_index()
# ChinaとUSは複数の州のデータがあるので国全体の合計にする
China_cumsum = China_pre_cumsum.groupby(['#date'])['#affected+infected+value+num'].sum()
US_cumsum = US_pre_cumsum.groupby(['#date'])['#affected+infected+value+num'].sum()
# 原系列の表示(感染者数の累積和)
plt.figure(figsize = (20,10))
ax = plt.subplot()
ax.plot(China_cumsum,label = "Total Confirmed in China")
ax.plot(US_cumsum,label = "Total Confirmed in US")
ax.plot(Italy_cumsum["#affected+infected+value+num"],label = "Total Confirmed in Italy")
ax.plot(Spain_cumsum["#affected+infected+value+num"],label = "Total Confirmed in Spain")
ax.plot(Germany_cumsum["#affected+infected+value+num"],label = "Total Confirmed in Germany")
ax.plot(Korea_cumsum["#affected+infected+value+num"],label = "Total Confirmed in Korea")
ax.plot(Japan_cumsum["#affected+infected+value+num"],label = "Total Confirmed in Japan")
plt.title('Coronavirus COVID-19',fontsize = 20)
plt.xlabel('date',fontsize = 20)
plt.ylabel('Total number of confirmed people',fontsize = 20)
plt.tick_params(labelsize=20)
plt.setp(ax.get_xticklabels(), rotation=90)
plt.legend(loc = "upper left",fontsize = 20)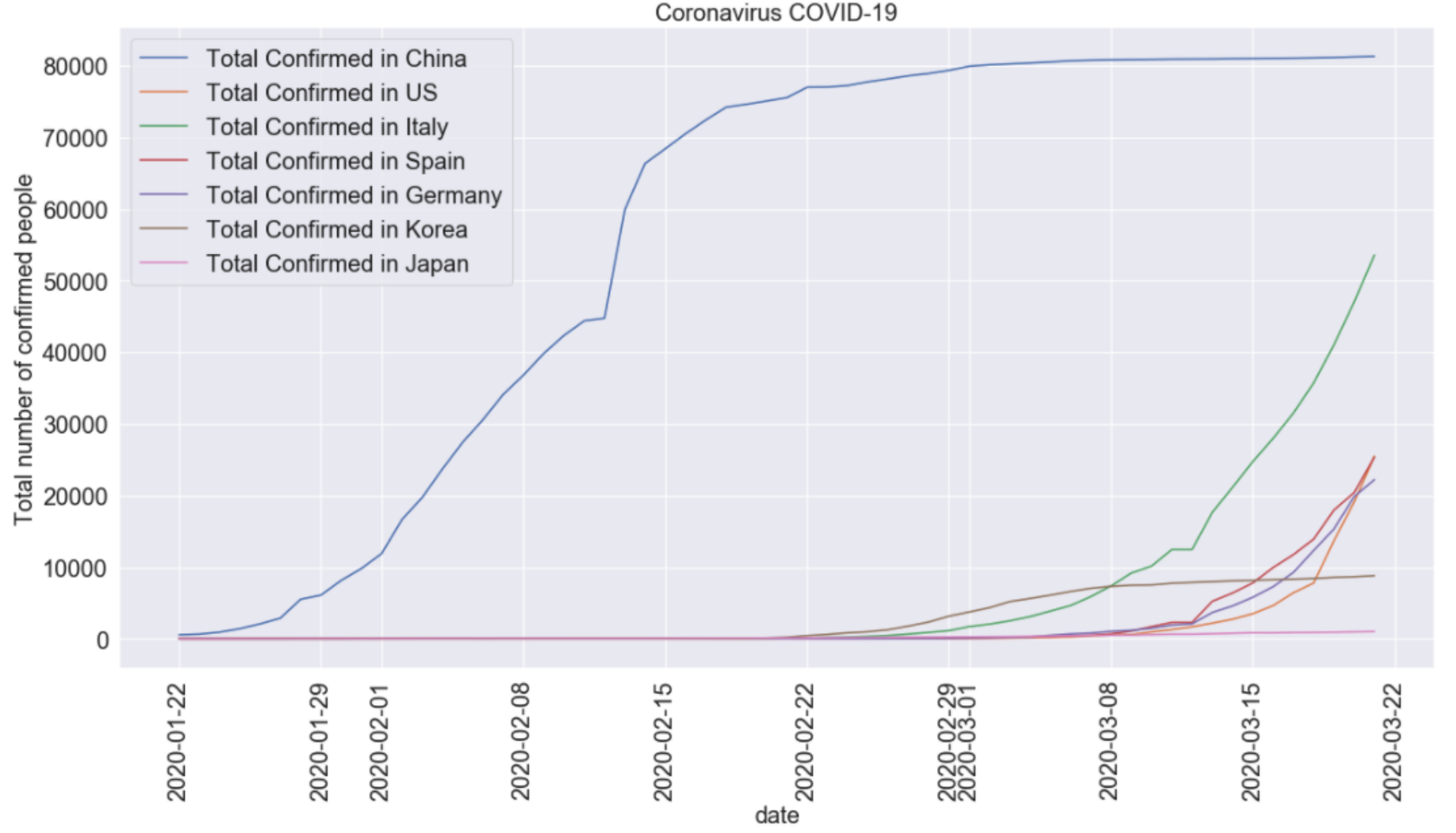
1/22 〜 3/21の各国の累積感染者数
今回使用したデータでは、中国と米国は州別にデータが入力されていたため、国全体の合計に変換しました。3/22時点では、中国の累積感染者数が最も多いですね。
日本、韓国だけを抜き出したのが以下のグラフです。
感染者数は増加傾向にあるものの、米国、イタリア、ドイツ、スペインに比べると明らかに傾きが緩いです。

累積感染者数から日本、韓国のみ抜粋
次に、上記のデータに対して1階差分を取り日毎の感染者数を算出します。
1/22は前日のデータがないため、データが消失します。
# 日毎の感染者数を求める(1階差分を取る)
# 日毎の感染者数が負になっている日はデータの誤りとして除いている
China_diff = China_cumsum.diff().dropna()
China_diff = China_diff[China_diff>=0]
US_diff = US_cumsum.diff().dropna()
US_diff = US_diff[US_diff>=0]
Italy_diff = Italy_cumsum["#affected+infected+value+num"].diff().dropna()
Italy_diff = Italy_diff[Italy_diff>=0]
Spain_diff = Spain_cumsum["#affected+infected+value+num"].diff().dropna()
Spain_diff = Spain_diff[Spain_diff>=0]
Germany_diff = Germany_cumsum["#affected+infected+value+num"].diff().dropna()
Germany_diff = Germany_diff[Germany_diff>=0]
Korea_diff = Korea_cumsum["#affected+infected+value+num"].diff().dropna()
Korea_diff = Korea_diff[Korea_diff >=0]
Japan_diff = Japan_cumsum["#affected+infected+value+num"].diff().dropna()
Japan_diff = Japan_diff[Japan_diff>=0]
#グラフの表示は累積感染者数と同じなので割愛
1/22 〜 3/21の日毎の感染者数
中国のデータに於いて、2/13に巨大なピークがあります。
これは湖北省が感染者の認定基準を変えたことによるものと思われます。
こういう場合データをどう扱うか悩みますが(汗)、一旦このまま分析を進めることにします。

中国湖北省に於ける認定基準の変更
日毎の感染者数で韓国、日本だけを抜き出したのが以下のグラフ。
韓国はピークを過ぎているが、日本は増加トレンドにあるように見えます。

日毎の感染者数から日本、韓国のみ抜粋
単位根検定を行う
前述したとおり、Varモデルは定常過程を前提としているため、過程が定常か調べておく必要があります。
これは単位根検定で調べることができます。単位根検定には主に以下の3つがあるようです。
原理は理解できていないので割愛しますが、対立仮説と帰無仮説の対応は以下のとおりです。
| 名称 | 帰無仮説 | 対立仮説 |
|---|---|---|
| Dickey-Fuller(DF)検定 | 単位根AR(1)過程である | 定常AR(1)過程である |
| 拡張DF(ADF)検定 | 単位根AR(p)過程である | 定常AR(p)過程である |
| Phillips-Perron(PP)検定* | 単位根AR(p)過程である | 定常AR(p)過程である |
(*ホワイトノイズの分散不均一性まで考慮した検定手法)
今回は日毎の中国、韓国、日本のデータに対してADF検定を行います。
結果は帰無仮説と対立仮説のモデルの置き方によって違ってくるため、3つのモデルを考えます。
表中のregressionは以下で行うstattools.adfullerのオプションのregressionに対応します。
$$δt$$は1次のトレンドを表ます。
# 中国の日毎の感染者数に対してADF検定を行う
# 出力値は先頭からt値、p値、使用されたラグの数、計算に使用されたデータ数、各棄却域に対するt値、AICの最大値
# トレンド項あり(2次まで)、定数項あり
ctt = stattools.adfuller(China_diff, regression="ctt")
# トレンド項あり(1次)、定数項あり
ct = stattools.adfuller(China_diff, regression="ct")
# トレンド項なし、定数項あり
c = stattools.adfuller(China_diff, regression="c")
# トレンド項なし、定数項なし
nc = stattools.adfuller(China_diff, regression="nc")
# 韓国、日本も同様に行う
日毎の感染者数に対する単位根検定のp値をまとめると以下のようになりました。
| 国 | 場合1 | 場合2 | 場合3 | 結論 |
|---|---|---|---|---|
| 中国 | 0.051 | 1.0e-4 | 4.4e-05 | 場合2,3を仮定すると定常過程と言える |
| 韓国 | 0.26 | 0.55 | 0.70 | いずれの場合も単位根過程でないとは言えない |
| 日本 | 0.74 | 0.80 | 2.7e-7 | 場合3を仮定すると定常過程と言える |
韓国のデータは定常過程と言えないので除外し、中国の感染者数と日本の感染者数のグレンジャー因果性だけを検定することにします。
Varモデルの構築
中国と日本の日毎の感染者数のデータでからVarモデルを構築します。
# 中国と日本のデータで共通する日付けのデータだけを抜き出す
diff_CJ = pd.merge(China_diff, Japan_diff, on='#date', how='inner')
# 列名を変更する
diff_CJ.columns = ["China_diff","Japan_diff"]
#Varモデルを作成する
model_diff = VAR(diff_CJ)
フィッティングにあたってモデルのラグ(1式のp)を決めてやる必要があります。
現時点から何時点過去に遡って回帰式を構成するかを決める作業です。
これは、情報量基準(AIC、BIC)を指標に決めます。
# 最適なラグを探索する。ラグ10まで
model_diff.select_order(10).summary()

各ラグに於ける情報量基準の計算
ラグ1まで考慮した場合に情報量基準が最小になりました。
実際は以下のようにmaxlags=10とic="aic"と指定してやることでラグ10までの範囲でAICが最小となるラグを自動的選んでフィッティングしてくれます。
# AIC基準で最適なラグを選択したモデルへのあてはめ
result_diff = model_diff.fit(maxlags=10, ic="aic")
#あてはめの結果を表示
result_diff.summary()

あてはめの結果
サマリーの中に記載されている係数を用いて、
中国の感染者数と日本の感染者数は以下のように書けます。


result_diff.test_causality("Japan_diff", "China_diff", kind = "f").summary()

グレンジャー因果性検定の結果
帰無仮説:
「中国の感染者数から日本の感染者数に対してグレンジャー因果性が存在しない」を棄却できませんでした。
したがって、昨日の中国の感染者数と今日の日本の感染者数にグレンジャー因果性がないと結論付けました。
この結果は以下を考えると妥当という気がします(分析手法が正しければですが、、)。
●1日という短期間で中国 → 日本間でウイルスの媒介が波及しそうにないこと
●感染が発覚した人のみのデータを使っているので相関が上手く拾えていない可能性があること
最後に
COVID-19の実データを使ってグレンジャー因果性検定をやってみましたが、かなり難しさを感じました。
テキストに付随するデータだとすんなり結論を導けるのですが、
実データとなると「そもそもこのモデルを使って良いデータなのか?前提条件を満たしているのか?」と言った疑念が浮かんできます(笑)。
実務やコンペなどで経験を積んで正しく分析できるようになりたいです。
参考文献
手法やコードは以下の書籍を参考にしました。
説明がコンパクトに纏まっていて非常に分かり易いです。

通称「沖本本」
https://www.amazon.co.jp/dp/4254127928/ref=cm_sw_em_r_mt_dp_YSJ0VBN3H4NQ88STYNE
Pythonによる時系列分析のコードが豊富です。

Advanced Python
