2021年6月20日に統計検定準1級を受験しました。
結果は不合格でしたが、CBTでの再挑戦に向けて解答をまとめていきます。
(⇒2021年8月にCBT試験に合格しました。受験体験記を書きましたので、良ければご覧ください😀)
あくまで、自作なので正解を保証するものではありません。また、導出過程で誤りがある可能性が多分にあります。
ご指摘は大歓迎ですので、よろしくお願いいたします。
本記事の内容
はじめに
問題と略解は一般財団法人 統計質保証推進協会のサイトで公開されています。
著作権法により、無断での問題の複製・転載が禁止されているので、問題はこちらに記載しません。上のリンクから参照ください。
2020年の試験が中止になったので、2年分をまとめた公式過去問題集が出版されるのはかなり先になると思われます、、
また、勉強、理解の都合上解答が順不同になります^_^;
選択問題 問8

- 概要:母比率の差の検定
- 参考:ワークブック10章P79~81、ワークブック11章P87
問題設定より、母分散$σ^2$が共通であることがキーになる。
また、明記されていなが、$μ_A$と$μ_P$は独立と考えて良い。母平均の差の検定であることに注意。
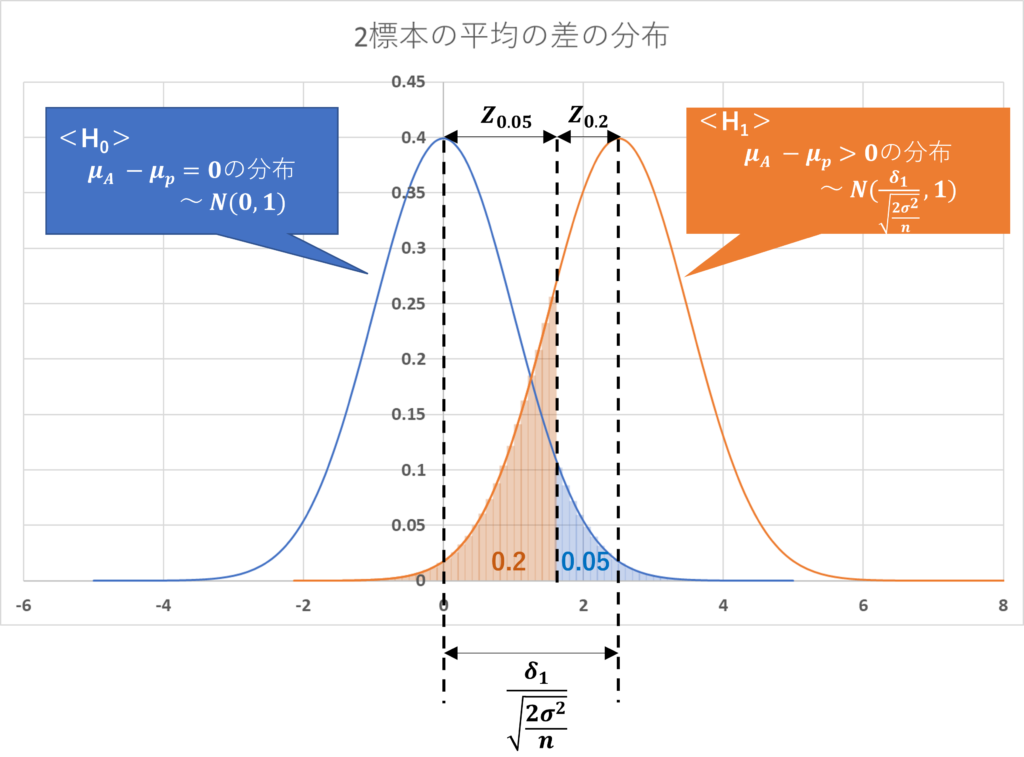
母平均の差の分布はそれぞれ、以下のようになります。
$H_0$ : 母平均の差 = 0 ($μ_A-μ_P=δ_0=0$)
$H_1$ : 母平均の差 > 0 ($μ_A-μ_P=δ_1>0$)
それぞれの場合に、母平均の差が従う確率分布は以下になります。
$H_0$ :~$ N(\frac{δ_0 - δ_0}{\sqrt{\frac{2σ^2}{n}}}, 1)$=~$ N(0, 1)$
$H_1$ :~$ N(\frac{δ_1 - δ_0}{\sqrt{\frac{2σ^2}{n}}}, 1)$=~$ N(\frac{δ_1}{\sqrt{\frac{2σ^2}{n}}}, 1)$
有意水準$α=5$%、検出力$(1-β)=80$%より、以下の図式が成立する。
また、下図より以下の関係式が成立する。
$$Z_{0.05}+Z_{0.2} =\frac{μ_A-μ_P(=δ_1)}{\sqrt{V(μ_A-μ_P)}}$$
$$2.49=\frac{μ_A-μ_P}{\sqrt{\frac{σ^2}{n}+\frac{σ^2}{n}}}・・・8-(1)$$
[1] 正解④
問題設定より、降圧薬Aの効果がプラセボ効果より大きいことを立証したいので、
帰無仮説:$μ_A=μ_P$ 、対立仮説:$μ_A>μ_P$
となる。
[2] 正解④
式8-(1)と矛盾する選択肢を消していけば良い。
①:有意水準($α$)を固定したまま、検出力($1-β$)を減少させると、式8-(1)の左辺は減少する。
したがって、右辺のnは減少することになる。よって、誤り。
②:有意水準($α$)を5%→1%にすると、式8-(1)の左辺は増加する。
したがって、右辺のnは増加する。よって、誤り。
③:式8-(1)右辺の分母より、$σ^2$が大きいほど、nは大きくなります。
よって、誤り。
④:式8-(1)右辺の分子=$δ$となるため、$δ$が小さいほど、nは大きくなります。
よって、正しい。
[3] 正解③
「必要症例数は両群合わせた数」であるというのが、注意点になります。
(※私は最後に2倍するのを忘れました)
式8-(1)に$δ_1=3.1$、$σ=4.2$を代入して解くと、$n=23$が得られます。
最後に2倍して$46$が答えになります。
部分記述問題 問2

- 概要:指数分布とデルタ法を組み合わせた問題
- 参考:ワークブック6章P40、7章P56
[1] 正解 $λ^2$
指数分布の分散だから、$λ^2$となる。
ワークブックP40の式、$f(x)=λe^{-λx}$と$λ$の定義が逆数の関係になっていることに注意。
[2] 正解 $(\frac{1}{n}\sum_{i=1}^n x_i)^2$
尤度関数は以下で表せる。
$$\prod_{i=1}^n \frac{1}{λ}exp(\frac{-x_i}{λ})$$
両辺の対数を取り、
$$nlog(\frac{1}{λ})-\sum_{i=1}^n \frac{x_i}{λ}$$
これを$λ$について微分し、=0とおいて$λ$を求めると、
$$λ=\frac{1}{n}\sum_{i=1}^n x_i$$
ゆえに、分散$θ$の最尤推定量は、
$$λ^2=(\frac{1}{n}\sum_{i=1}^n x_i)^2$$
[3] 正解 $4λ^4$
デルタ法より、以下が成立する。
$$\sqrt{n}((\frac{1}{n}\sum_{i=1}^n x_i)^2 - λ^2) ~ N(0, ((λ^2)')^2×λ^2)$$
$$=N(0, 4λ^4)$$
ゆえに、最尤推定量の漸近分散は$4λ^4$となる。
部分記述問題 問1

- 概要:条件付き確率と事象に関する問題
- 参考:現代数理統計学の基礎 第1章演習問題問2
[1]正解0.4
ベイズの定理より、
$$P(A|B)$$
$$=\frac{P(A(\cap)B)}{P(B)}$$
$$=\frac{P(A)+P(B)-P(A(\cup)B)}{P(B)}$$
$$=\frac{0.45+P(B)-0.65}{P(B)}$$
これを、$P(B)$について解いて、$P(B)=0.4$を得る。
[2]正解0.85
$$P(A(\cup)B(\cup)C)$$
$$=P(A)+P(B)+P(C)-P(A(\cap)B)$$
$$-P(A(\cap)C)-P(B(\cap)C)+P(A(\cap)B(\cap)C)$$
$$=0.45+0.4+0.45-0.2-0.2-0.1+0.05$$
$$=0.85$$
論述問題 問2

- 概要:ベイズ法で事後分布、母数を求める問題
観測値から事後分布を更新する問題
CBT移行後も頻出と思われる - 参考:ワークブック31章P296 例1
データ解析のための統計モデリング入門9章
[1-1]正解(A)、(B)
代表的な母数と共役事前分布の組み合わせは以下のとおり。
| 母数 | 共約事前分布 |
| 正規分布の平均$μ$ | 正規分布 ※[2]のケース |
| 正規分布の分散$σ^2$ | 逆ガンマ分布 |
| ガンマ分布の母数 | ガンマ分布 |
| 二項分布の生起確率$p$ | ベータ分布 ※[1]のケース |
| 多項分布の生起確率$p_{j}$ | ディリクレ分布 |
| ポアソン分布の平均$λ$ | ガンマ分布 |
ゆえに、正しい組合せは(A)、(B)
[1-2]正解$α_{1}=α_0+x_0、β_1=n+β_0-x_0$
ベイズの定理より、
$Be(α_1,β_1)=Bin(n,θ) \times Be(α_0,β_0)$
$={}_n \mathrm{C}_X \times θ^{X} \times (1-θ)^{n-X} \times$
$\frac{1}{B(α_0,β_0)} \times θ^{α_0-1} \times (1-θ)^{β_0-1}$
$\propto θ^{x_0+α_0-1} \times (1-θ)^{n-x_0+β_0-1}$
$\propto Be(x_0+α_0,n-x_0+β_0)$
ゆえに、$α_1=x_0+α_0$、$β_1=n-x_0+β_0$である。
[1-3]正解$θ=\frac{x_0+α_0-1}{n+α_0+β_0-2}$
[1-1]で求めた、
事後分布$Be(x_0+α_0,n-x_0+β_0) \propto θ^{α_1-1} \times (1-θ)^{β_1-1}$を最大にする$θ$を求める。
上式を$θ$で微分して、=0と置き、$θ$について解くと、
$$θ=\frac{α_1-1}{α_1+β_1-2}$$
$$=\frac{x_0+α_0-1}{n+α_0+β_0-2}$$
[別解]
事後分布を最大にする$θ$の推定量はMAP推定量(=事後分布の最頻値)である。なので、$Be(α_1,β_1)$の最頻値を求めれば良い。
ベータ分布のパラメーター $Be(α,β)$において、
平均$=\frac{α}{α+β}$
分散$=\frac{αβ}{(α+β)^2(α+β+1)}$
最頻値$=\frac{α-1}{α+β-2}$
ゆえに、$θ=\frac{α_1-1}{α_1+β_1-2}$
[2-1]$N(\frac{3}{5},\frac{4}{5})$ ⇒ (B)
ベイズの定理と、問題設定より、
$$事後分布=N(μ|X_1=3.0, σ^2=4) \times N(0,1)$$
$$=N(\frac{3}{5},\frac{4}{5})$$
(B)のグラフが該当する。ただし、以下の公式を用いた。 正規分布の積 $N(μ_1,σ^2_1) \times N(μ_2,σ^2_2)$の分布は、 平均$=\frac{μ_1σ^2_2+μ_2σ^2_1}{σ^2_1+σ^2_2}$
以下の母数を持つ正規分布になる。
分散$=\frac{1}{σ^2_1+σ^2_2}$
[2-2]$N(\frac{11}{8},\frac{1}{2})$
ベイズの定理と、問題設定より、
事後分布
$=N(μ|X_2=2.3, σ^2=4) \times$
$N(μ|X_3=4.2, σ^2=4) \times $
$N(μ|X_4=1.5, σ^2=4) \times $
$N(\frac{3}{5},\frac{4}{5})$
$=N(\frac{11}{8},\frac{1}{2})$
(上記の公式を繰り返し使用)
選択問題 問3

- 概要:多変量正規分布の母数と条件付き分布を求める問題
ワークブックに2変量の演習はあるが、3変量以上はノーマークだった、、 - 参考:ワークブック6章P43~P44
[1]正解⑤
確率分布$X+Y$、$Y-Z$について、期待値、分散、共分散を求める。
$E(X+Y)=E(X)+E(Y)=1+2=3$
$V(X+Y)=V(X)+V(Y)+2Cov(X,Y)$
$=2+3+2 \times 0 = 5$
$E(Y-Z)=E(Y)-E(Z)=2-3=-1$
$V(Y-Z)=V(Y)+V(Z)-2Cov(Y,Z)$
$=3+4-2 \times 2 = 3$
(この時点で⑤を選べるが、共分散まで求める)
$Cov(X+Y,Y-Z)$
$=E[(X+Y)(Y-Z)]-E(X+Y)E(Y-Z)$
$=E(XY-XZ+Y^2-YZ)+3$
$=Cov(X,Y)+E(X)E(Y)-Cov(X,Z)$
$-E(X)E(Z)+V(Y)+E(Y)^2-Cov(Y,Z)$
$-E(Y)E(Z)+3$
$=0+2-1-3-+3+4-2-6+3$
$=0$
ゆえに、⑤が正解
[2]正解⑤
こちらは、自力で解けなかったので@alo4phaさんの解答を参考にさせていただきました。
※$ρ(xz)$は$X$と$Y$の相関係数を意味します。
$E(Z|X=x,Y=y)$
$=μ_z+ρ(xz) \times \frac{σ_Z}{σ_X}(x-μ_X)+ρ(yz) \times\ \frac{σ_Z}{σ_Y}(y-μ_Y)$
$=3+\frac{1}{2}(x-1)+\frac{2}{3}(y-2)$
$=\frac{1}{2}x+\frac{2}{3}y+\frac{7}{6}$
$V(Z|X=x,Y=y)$
$=σ_Z^2(1-ρ(xz)^2-ρ(yz)^2)$
$=4 \times\ [1-(\frac{1}{\sqrt{2 \times 4}})^2-(\frac{2}{\sqrt{3 \times 4}})^2]$
$=\frac{13}{6}$
選択問題 問4

- 概要:単回帰分析の推定量に関する問題
切片の無い単回帰であることに注意
[2]、[3]は自信ない、、 - 参考:ワークブック16章
[1-1]正解③
正規方程式$\boldsymbol{X^{T}X}b=\boldsymbol{X^{T}Y}$より、
$b=\boldsymbol{(X^{T}X)^{-1}X^{T}Y}$
$=\frac{69.88}{30.39}$
$=2.3$ ⇒③
[1-2]正解③
回帰分析における、分散の不偏推定量は以下で表せる。
回帰分析における分散の不偏推定量 $\frac{Se}{n-k}$
$Se$:残渣平方和、$k$:説明変数の数+切片の数(本問では、切片ないので0)
(本例では$k=1$)
以下のように、残渣平方和を求めて5で割ると$2.07$となり、③を選べる。
| $Y$ | $b\boldsymbol{X}$ | 残差 |
| 0.1 | 2.53 | 5.90 |
| 2.7 | 2.76 | 0.0036 |
| 3.3 | 4.37 | 1.14 |
| 8.0 | 6.21 | 3.20 |
| 6.2 | 6.44 | 0.058 |
| 7.1 | 6.9 | 0.040 |
| 合計 | 10.34 |
[2]正解②
(A)ガウス・マルコフの定理より正しいと言えそう。
$b_1=\boldsymbol{c^{T}Y}$という推定量を考えると、
$E(b_1)=E(\boldsymbol{c^{T}Y})=bE(\boldsymbol{c^{T}X})=b$
上式を満たすのは、$\boldsymbol{c^{T}X}=1$の時である。
(B)ガウス・マルコフの定理が成り立つ時は、最小二乗推定量が最良線形不偏推定量(BLUE)
である。しかし、問題からはガウス・マルコフの定理が成り立つことは読み取れない。
(問題文に「説明変数と誤差項が独立」と書かれていないので)
したがって、$b$がBLUEとは言えないので誤り。
[3]正解①
こちらもよく分かりません、、^_^;
重回帰分析における偏回帰係数の検定、帰無仮説:$b_1=b_2=....=b_d=0$の拡張と考えました。
統計検定量は、(ワークブックP131より)
$$T=\frac{5(||\boldsymbol{X}b-\bar{y}||)^2}{(\boldsymbol{Y}-b\boldsymbol{X})^T(\boldsymbol{Y}-b\boldsymbol{X})}~F(1,5)$$
$F_{0.05}(1,5)=6.608$より選択肢①、④に絞れる。さらに、上式と近い形である①を選ぶ((笑))
選択問題 問5

グラフから値を読み取り、決定係数を計算する必要がある。
モニターから数値を読み取るのは厳しいため、CBT移行後、数値読み取り問題は減りそう。
[1]正解②
①:最小二乗推定量も一般化最小二乗推定量も不偏推定量であるため、バイアスは0である。したがって誤り。
②:最小二乗推定量の分散より、一般化最小二乗推定量の分散は小さいので正しい。
(詳細は、計量経済学講義ノートを参照)
③:一般化最小二乗推定量は誤差分散を独立を仮定しておらず、計算は複雑になると思われる。したがって、誤り。
④:問題文中の図より、最小二乗法に比べて一般化最小二乗法の残渣平方和が小さいようには見えない。したがって、誤り。
⑤:正則化項が無いことから、Ridge回帰、Lasso回帰のような性質は無いと思われれる。したがって、誤り。
[2]正解②
決定係数の定義より②を選べる 決定係数 $R^2=\frac{\sum_{i=1}^{10}(\hat{y_i}-\bar{y})^2}{\sum_{i=1}^{10}(y_i-\bar{y})^2}=1-\frac{\sum_{i=1}^{10}(y_i-\hat{y_i})^2}{\sum_{i=1}^{10}(y_i-\bar{y})^2}$
[3]正解④
グラフから値を読み取り、上式に代入すれば答えが求まる。
グラフから(私が)読み取った値は以下のとおり、
| y | 最小二乗法$\hat{y_i}$ | 一般化最小二乗法$\hat{y_i}$ |
| 190 | 175 | 185 |
| 190 | 185 | 190 |
| 210 | 210 | 212 |
| 220 | 240 | 240 |
| 240 | 250 | 245 |
| 250 | 260 | 250 |
| 260 | 270 | 260 |
| 290 | 290 | 275 |
| 300 | 300 | 290 |
| 360 | 330 | 310 |
上の表より、
$\bar{y}=251 , \sum_{i=1}^{10}(y_i-\bar{y})^2=26090$
- 最小二乗法
$\sum_{i=1}^{10}(y_i-\hat{y_i})^2=1850$
$R^2=0.929$ - 一般化最小二乗法
$\sum_{i=1}^{10}(y_i-\hat{y_i})^2=3279$
$R^2=0.874$
一般化最小二乗法の決定係数が選択肢と大きくずれているが、大小関係が一致し、最小二乗法の決定係数の近しい④を選んだ。
最小二乗法の決定係数のほうが大きくなっていることからも、[1]の選択肢④が誤りであることが分かる。
部分記述問題 問12

検定統計量は与えられているので、正しく棄却域を決められ、
相関係数を計算できれば解ける。
[1] 正解 2.45
帰無仮説:母相関係数=0、対立仮説:母相関係数≠0
有意水準5%の両側検定となる。
ゆえに、棄却域は
$t_{0.025}(6)=2.447≒2.45$
無相関の検定統計量 $T=\frac{|R|\sqrt{n-2}}{\sqrt{1-R^2}}~t(n-2)$ 本例では、$n=8$、有意水準5%なので、 余談ですが、ビッグデータ($n$大)に対して検定を行うと$R$が小さくても帰無仮説が棄却されてしまうため注意が必要です。
($R$:相関係数、$n$:サンプル数)
$T=\frac{\sqrt{6R^2}}{\sqrt{1-R^2}}~t_{0.025}(6)$
[2] 正解 2.47
相関係数を求めて、上式$R$に代入する。
$R=\frac{\sum_{i=1}^{8}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^{8}(x_i-\bar{x})^2\sum_{i=1}^{8}(y_i-\bar{y})^2}}=\frac{5.91}{\sqrt{7.16 \times 9.68}}=0.710$
$T=\frac{\sqrt{6 \times 0.71^2}}{\sqrt{1-0.71^2}}=2.47$
選択問題 問10

スペクトラムは過去4年出ていなかったので、ノーマーク、、
[3]は、背後に共分散が隠れているので丁寧な計算が必要
[1]正解①
[コレログラムの算出]
1次の自己相関係数を計算する。
$\gamma_1 = Cov(y_t,y_{t-1})=E[(y_t)(y_{t-1})]$
$=E[(\epsilon_{t}+0.8\epsilon_{t-1})(\epsilon_{t-1}+0.8\epsilon_{t-2})]$
$=0.8E[(\epsilon_{t-1})^2]$
$=0.8σ^2$
(※$E(y_t)=E(y_{t-1})=0$であることを用いた)
一方、分散は、
$\gamma_0 =V(\epsilon_{t}+0.8\epsilon_{t-1})=V(\epsilon_{t})+0.8^2V(\epsilon_{t-1})$
$=1.64σ^2$
ゆえに、$\rho_1=\frac{\gamma_1}{\gamma_0}=0.49$ ⇒この時点で①、②に絞れる。
[スペクトル密度関数の算出]
本例の場合、MA(1)のスペクトル密度関数は以下で計算できる。
$f(λ)=\frac{σ^2}{2\pi}[(1+0.8e^{iλ})(1+0.8e^{-iλ})]$
$=\frac{σ^2}{2\pi}(1+0.8e^{-iλ}+0.8e^{iλ}+0.8^2)$
$=\frac{σ^2}{2\pi}(1+2 \times 0.8cosλ+0.8^2)$
$=\frac{σ^2}{2\pi}(1.64+1.6cosλ)$
⇒λ=0の時最大値を取るので、①を選べる。
[2]正解③
[コレログラムの算出]
1次の自己相関係数を計算する。
$\gamma_1=Cov(y_t,y_{t-1})=E[(y_t)(y_{t-1})]$
$=E(-0.8y_{t-1}^2+\epsilon_{t}y_{t-1})$
$=-0.8E(y_{t-1}^2)+E(\epsilon_{t}y_{t-1})$
$=-0.8E(y_{t-1}^2)=-0.8\gamma_0$
(※$E(y_t)=E(y_{t-1})=0$であることを用いた)
ゆえに、$\rho_1=\frac{\gamma_1}{\gamma_0}=-0.8$ ⇒この時点で③、④に絞れる。
[スペクトル密度関数の算出]
本例の場合、AR(1)のスペクトル密度関数は以下で計算できる。
$f(λ)=\frac{σ^2}{2\pi}\frac{1}{(1+0.8e^{iλ})(1+0.8e^{-iλ})}=\frac{σ^2}{2\pi}\frac{1}{1+0.8e^{-iλ}+0.8e^{iλ}+0.8^2}$
$=\frac{σ^2}{2\pi}\frac{1}{1+2 \times 0.8cosλ+0.8^2}=\frac{σ^2}{2\pi}\frac{1}{1.64+1.6cosλ}$
⇒λ=$\pi$の時最大値を取るので、③を選べる。
試験では時間が無いので、以下を暗記しておいたほうが良いと思われる。
AR(1)過程の自己共分散、自己相関 $\gamma_1=\varphi_{1}\gamma_{0}=\varphi_{1}\frac{σ^2}{1-\varphi_{1}^2}$ $\gamma_h=\varphi_{1}^h\gamma_0$
($\gamma_0$:分散 $\varphi_{1}$:ラグ1の項の係数)
$\rho_1=\frac{\gamma_1}{\gamma_0}=\varphi_{1}$
$\rho_h=\frac{\gamma_h}{\gamma_0}=\varphi_{1}^h$
[3]正解③
こちは、私は何回計算しても$1$になりました。$V(\bar{y_n})$の中に現れる共分散を見逃していました、、
$nV(\bar{y_n})=\frac{1}{n}V(\sum_{t=1}^{n}y_t)$
$=\frac{1}{n}[(\epsilon_1+0.8\epsilon_0)+(\epsilon_2+0.8\epsilon_1)+......$
$+(\epsilon_{n-1}+0.8\epsilon_{n-2})+(\epsilon_n+0.8\epsilon_{n-1})]$
$=\frac{1}{n}[nV(\epsilon_t)+nV(0.8\epsilon_t)+2(n-1)Cov(\epsilon_t,0.8\epsilon_t)]$
$=\frac{1}{n}[nσ^2+0.64nσ^2+1.6(n-1)σ^2]$
$=1.64σ^2+1.6(1-\frac{1}{n})σ^2$
$V(y_t)=V(\epsilon_t+0.8\epsilon_{t-1})$
$=σ^2+0.8^2σ^2$
$=1.64σ^2$
$\lim_{n \to \infty}\frac{nV(\bar{y_n})}{V(y_t)}$
$=\lim_{n \to \infty}\frac{1.64σ^2+1.6(1-\frac{1}{n})σ^2}{1.64σ^2}$
$=\frac{3.24}{1.64}=1.98$
[4]正解④
以下の関係を使って、連立方程式を立てて解けば求まります。
AR(2)過程において、
$\rho(1)=a_1+a_2\rho(1)=a_1+0.5a_2$
$\rho(2)=a_1\rho(1)+a_2=0.5a_1+a_2$
これを解くと、$a_1=0.83 , a_2=-0.67$と求まります。
AR(p)過程のラグhの自己共分散、自己相関 $\gamma_h=\varphi_{1}\gamma_{h-1}+\varphi_{2}\gamma_{h-2}+....+\varphi_{p}\gamma_{h-p}$ $\rho_h=\frac{\gamma_h}{\gamma_0}=\varphi_{1}\rho_{h-1}+\varphi_{2}\rho_{h-2}+....+\varphi_{p}\rho_{h-p}$ (上の連立方程式では、$\rho_0=1, \rho_{-1}=\rho_{1}$の関係を使っている)
($\varphi_{1}$:ラグ1の項の係数)
($\gamma_0$:分散)
選択問題 問9

基本事項を理解していれば、ノー計算で直感的に選択肢選べそう
日本統計学会公式認定 統計検定1級対応「統計学」P177~P179
[1]正解④
解答のキーになるのは以下の文言
- 1番目から5番目の項目はある因子を、
6番目から10番目の項目はそれぞれ別の因子を測定する- 因子間には中程度の負の相関があることが分かっている
- 「データを同じ回答カテゴリにばかり回答した回答者(これをA群とする)」と
「そうでない回答者(B群とする)」
$1、3.$より、B群は2因子であることが分かる。したがって、B群のスクリープロットは2である。
$1.$より、B群は1~5番目、6~10番目で因子負荷量がはっきり分かれていると思われる。
これに該当する因子パターンは1である(1~5番目が因子2、6~10番目が因子1)。
$2.$より、B群の因子間には負の相関があるから、因子間相関2が選べる。
⇒該当するのは④
[2]正解③
逆転項目では、因子負荷量が他の項目と符号違いになる。
因子パターン1の1~5番目、6~10番目にそれぞれ注目すると、符号が逆になっている組み合わせは
項番2,3,6 又は、項番1,4,5,7,8,9,10 。選択肢で選べるのは項番2,3,6の③。
[3]正解⑤
消去法で絞れなかったので、確実に言えそうな選択肢を選ぶ。
A群の因子間には元々強い正の相関があった。そのA群のデータをB群に混ぜて、
全データで因子負荷量を求めると、B群の1~5番目において、正の相関
(逆転項目になっていない組)の相関は強められると考えた。
以上を表しているのは⑤(?)
選択問題 問7

AICの定義、AIC、BICの性質の違いを知っていれば単純な計算で解ける
[1-1]正解④
線形回帰モデル1は以下のように、正規分布で表せる(ワークブックP289 (30.1式))。
$N(\beta_0+\beta_1x_{t1}+\beta_2x_{t2}+\beta_3x_{t3} , \sigma^2)$
$=\frac{1}{\sqrt{2π}\sigma}exp[-\frac{(y_t-(\beta_0+\beta_1x_{t1}+\beta_2x_{t2}+\beta_3x_{t3}))^2}{2\sigma^2}]$・・・①式
$X=\frac{y_t-(\beta_0+\beta_1x_{t1}+\beta_2x_{t2}+\beta_3x_{t3})}{\sigma}$
と置くと、
①式$=\frac{1}{\sigma}\frac{1}{\sqrt{2π}}exp(-\frac{X^2}{2})$
$=\frac{1}{\sigma}\phi(X)$
⇒④が選べる
[1-2]正解①
最大対数尤度を以下の式に当てはめてAICを計算し、AICが最も小さくなるモデルを選ぶ。
AIC $AIC=-2logL+2k$ 本問いでは使いませんが、以下の残差平方和を使って計算する問題もよく出ます。 $AIC=n(logSe+log\frac{2\pi}{n}+1)+2k$ モデル1の場合、k=3(説明変数の数)+2(切片$\beta_0$と$\sigma^2$)=5 になります。
($logL$:最大対数尤度、$k$:推定するパラメーター数)
($n$:サンプル数、$Se$:そのモデルでの残差平方和、$k$:推定するパラメーター数)
問題で与えられている最大対数尤度とパラメータ数からAICを計算すると以下のようになります。
| 候補モデル | AIC |
| モデル1 | 1695.8 |
| モデル2 | 1928.8 |
| モデル3 | 1698.8 |
| モデル4 | 1911.2 |
| モデル5 | 2038.3 |
| モデル6 | 2008.0 |
| モデル7 | 1930.1 |
AICが最も小さいモデル1を選びます。
[1-3]正解②
kaggleなどでお馴染みのクロスバリデーションに関する問題。
予測誤差が最も小さいモデル3を選びます。
[2]正解③
AIC、BIC、クロスバリデーションの性質(というほどの知識ではない)を知っていれば解答できます。
- BICは、$n→∞$の時、確率1で真のモデルを選択する
- クロスバリデーションは計算を繰り返すので、AIC、BICよりも計算量が嵩む
この2点から、手法(A)はBIC、手法(C)はクロスバリデーションと分かる。
これを満たすのは選択肢③
選択問題 問11

オートエンコーダと確率的勾配法の説明はワークブックに全くないが、
知っていれば知識だけで解ける。
G検定時の記憶を駆使して選びました。
[1]正解③
文字1、2、7の重心を計算して、最も適当な図を選ぶ。
文字1の重心:
$PC1=\frac{-6.57-7.86-7.41}{3}=-7.28$
$PC2=\frac{0.12+1.03+0.48}{3}=0.54$
文字2の重心:
$PC1=\frac{6.31+6.72-0.24}{3}=4.26$
$PC2=\frac{9.84+1.22+6.28}{3}=5.78$
文字7の重心:
$PC1=\frac{2.94+1.24+8.04}{3}=4.07$
$PC2=\frac{-8.52-7.54-9.53}{3}=-8.53$
⇒③の図が最も合致していそう。
[2]正解①
ニューラルネットとオートエンコーダついて知っていれば、解ける。
[3]正解①
確率的勾配法について知っていれば、解ける。
選択肢①以外は$t+1$時点の更新式に$t+1$時点の偏微分が入っており、おかしい。
選択問題 問6

ワークブックに載っていない形式の問題で、はじパタを参考にしました。
はじめてのパターン認識6章 6.3線形判別分析
[1]正解②
はじパタのP85(6.49式)を参考に式変形していきます。
式変形を簡単にするために$n$倍して考えます。
$\mu_1=\bar{x} , \mu_2=\bar{y}$
$C_1$はグループ1を、$C_2$はグループ2を表します。
$nS=\sum\limits_{i=1}^{n} (z_i-\bar{z})(z_i-\bar{z})^T$
$=\sum\limits_{k=1}^{2} \sum\limits_{i \in C_k}^{} (z_i-\mu_k+\mu_k-\bar{z})(z_i-\mu_k+\mu_k-\bar{z})^T$
$=\sum\limits_{k=1}^{2} \sum\limits_{i \in C_k}^{}(z_i-\mu_k)(z_i-\mu_k)^T+\sum\limits_{k=1}^{2} n_k(\mu_k-\bar{z})(\mu_k-\bar{z})^T$
$=\sum\limits_{i=1}^{n_1} (x_i-\bar{x})(x_i-\bar{x})^T+\sum\limits_{i=1}^{n_2} (y_i-\bar{y})(y_i-\bar{y})^T$
$+n_1(\bar{x}-\bar{z})(\bar{x}-\bar{z})^T+n_2(\bar{y}-\bar{z})(\bar{y}-\bar{z})^T$
$=n_1S_1+n_2S_2+nS_B$
$=nS_W+nS_B$
両辺を$n$で割って、
$S=S_W+S_B$ を得る。⇒②
計算している時間はないので、以下を暗記しておくと良いと思います。
全分散、クラス内分散、クラス間分散の関係 $S=S_W+S_B$
$S$:全分散(全データの分散)
$S_W$:クラス内分散(クラス内の分散の合計値)
$S_B$:クラス間分散(全データの重心から見た各クラスの重心のばらつき)
[1]正解②
フィッシャーの線形判別分析では、
$J(\mathbf v)=\frac{\mathbf v^T S_{B} \mathbf v}{\mathbf v^T S_{W} \mathbf v}$・・・①を最大化する$\mathbf v$を求めて、
新たなデータ$\mathbf z_0$を変換した値$\mathbf v^T z_0$によって判別が行われる。
①式を最大化する$\mathbf v$はラグランジュの未定乗数法により、
$S_B\mathbf v = \lambda S_W\mathbf v$ ・・・②($\lambda$:固有値)
を解くことで得られることが分かっている。
$S_W$が正則であれば(逆行列を持てば)、②式は、
$S_W^{-1} S_B\mathbf v = \lambda\mathbf v$と書けるので、固有値を計算する行列は$S_W^{-1} S_B$、線形判別に用いる固有ベクトルは$\mathbf v$であり、これらを求めればよい。
$S_W^{-1} S_B$
$=\frac{1}{4 \times 3 - 2 \times 2} \begin{pmatrix} 3 & -2 \\-2 & 4 \end{pmatrix} \begin{pmatrix} 4 & 2 \\2 & 1 \end{pmatrix}$
$=\begin{pmatrix} 1 & 1/2 \\0 & 0 \end{pmatrix}$
次に固有ベクトル$\mathbf v$を求める。
$S_W^{-1} S_B \mathbf v = \lambda\mathbf v$
$(S_W^{-1} S_B - \lambda I_n)\mathbf v = 0$
$|S_W^{-1} S_B - \lambda I_n|=0$
$|\begin{pmatrix} 1-\lambda & 1/2 \\0 & -\lambda \end{pmatrix}| = 0$
$-\lambda(1-\lambda) = 0$
より、$\lambda = 0 , 1$
$\lambda = 1$の場合について、固有ベクトル$\mathbf v$を求める。
$\mathbf v = \begin{pmatrix} a\ \\ b \end{pmatrix}$と置くと、
$\begin{pmatrix} 1 & 1/2 \\0 & 0 \end{pmatrix} \begin{pmatrix} a\ \\ b \end{pmatrix} = \begin{pmatrix} a\ \\ b \end{pmatrix}$
$\begin{pmatrix} a\ \\ b \end{pmatrix} = k\begin{pmatrix} 1\ \\ 0 \end{pmatrix}$ ($k$:定数)
これらを満たすのは②である。