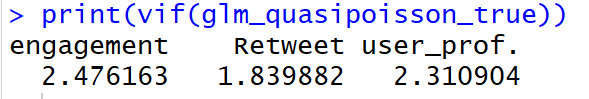
はじめに
統計検定の受験勉強が終わり、学習した手法を身近なデータで試したくなってきました。
そこで、15カ月分のツイートデータを数理統計学の手法を使って解析し、フォロワーを増やすための知見を得ることにトライしました。
フォロワーを増やすには、何を指標にすれば良いんだろうか?
いいね数?エンゲージメント数?
お断り
統計学の知識が浅いため、誤り、検討不足の可能性が大いにあります😅。
ブログコメント、Twitterなどでご指摘いただければ幸いです。
また、一般的な傾向ではなく、私のツイートデータでの結果になります。
本記事の内容
3行まとめ
まとめ
リツイート数が1増えると、フォロワー増加数は平均3.4倍に。
「多重共線性、過分散、割り算値をモデリングしてしまう」といった
落とし穴にはまりました😅
悪戦苦闘しましたが、良い勉強になりました。
ところで、
リツイートされ易いツイートてどんなだろう?
分析目的
フォロワーを増やすための指標作りが目的になります。
具体的には、
「説明変数$X$が〇〇増えるツイートをすると、フォロワーが1人増える(OR 〇〇倍)」
$X$の特定と、○○の数値を統計モデリングを使って求めたいと思います。
データの入手
以下のデータを入手しました。
入手方法は以下です。
- アナリティクス(Twitterの標準機能)
ホーム画面 ⇒ ①もっと見る ⇒ ②アナリティクス ⇒ ③全てのツイートアクティビティを表示 ⇒ ④データをエクスポート
この方法で、ツイートごとのデータがCSVで入手できます。
- socialdog(無料プランンで使える機能のみ)
ログインした画面で右上の期間を変えながら表示される値を記録しました。
注意点としては、登録後からデータが蓄積されるので、登録直後はデータが溜まっていないということです。登録 ~ 分析の間に一定期間必要になります。
(※無料プランの場合です、有料プランの場合は違う可能性があります)
データを記録する前に、左上のボタンで最新のデータを取得しておきましょう。
データの成形
データの成形にはPythonを使いました。
以下の期間のデータを入手しました。
| 期間 | フォロワー数 | |
| No.1 | 2020年4月 ~ 2021年3月 | 300 ⇒ 1100 |
| No.2 | 2021年9月 ~ 2021年11月 | 1900 ⇒ 2100 |
途中の空白期間はsocialdogにログインしていなかったため、データの保存が止まっており、取得できなかった期間になります。
ダウンロードしたCSVファイルを全て連携して、1つのデータフレームにします。
# 必要なライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import glob
from scipy.stats import poisson
from statsmodels.sandbox.regression.predstd import wls_prediction_std
from decimal import Decimal, ROUND_HALF_UP, ROUND_HALF_EVEN
import statsmodels.api as sm
from functools import partial
# 各種設定
sns.set(font='Yu Gothic', font_scale=2)
pd.set_option('display.max_columns', 50)
pd.set_option('display.max_rows', 50)
# CSVフィルの読み込み
csv_files = glob.glob('*ja.csv')
df_list = []
for filename in csv_files:
df = pd.read_csv(filename, encoding="cp932")
df_list.append(df)
# 縦に連結する
df = pd.concat(df_list, axis=0)
# 時間をインデックスに設定、ソートしておく
df['時間'] = pd.to_datetime(df['時間'])
df.set_index('時間', inplace=True)
df.sort_index(inplace=True)
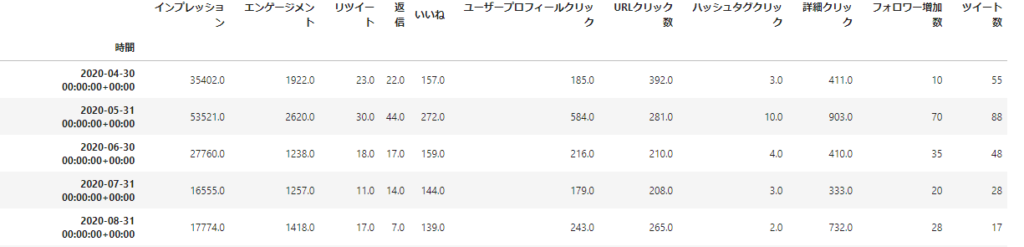
print(df.head())
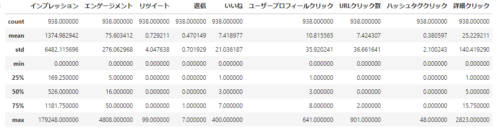
# 要約統計量 (見てみただけ、、)
print(df.describe())
# 分析に必要そうな列だけに絞る
df = df.loc[:,['ツイート本文', 'インプレッション', 'エンゲージメント',
'リツイート', '返信', 'いいね', 'ユーザープロフィールクリック', 'URLクリック数', 'ハッシュタグクリック',
'詳細クリック']]
def scatter_plot(X, y, var_names):
"""散布図を描く関数
Args:
X (int) :X軸の変数
y (int) :y軸の変数
var_names (list) :変数名を格納したリスト
Returns:
None
"""
lowess_plot = partial(
sns.regplot,
lowess=False,
robust=False,
ci=None,
scatter_kws={"s":50, "alpha":0.5},
line_kws={"linewidth": 1, "linestyle":"--"})
fig, ax = plt.subplots(figsize=(4,4), dpi=150)
lowess_plot(x=X, y=y, ax=ax)
ax.set_xlabel(var_names[0],fontsize=12)
ax.set_ylabel(var_names[1],fontsize=12)
ax.tick_params(axis='x', labelsize=10)
ax.tick_params(axis='y', labelsize=10)
ax.set_xlim(0, None)
fig.suptitle("「" + var_names[0] + " vs " + var_names[1] + "」" + " の散布図", fontsize=13)
plt.rcParams['figure.subplot.left'] = 0.15
fig.savefig(r"散布図の保存先パス" + var_names[0] + " vs " + var_names[1] + "の散布図" + ".png",
pad_inches=0)
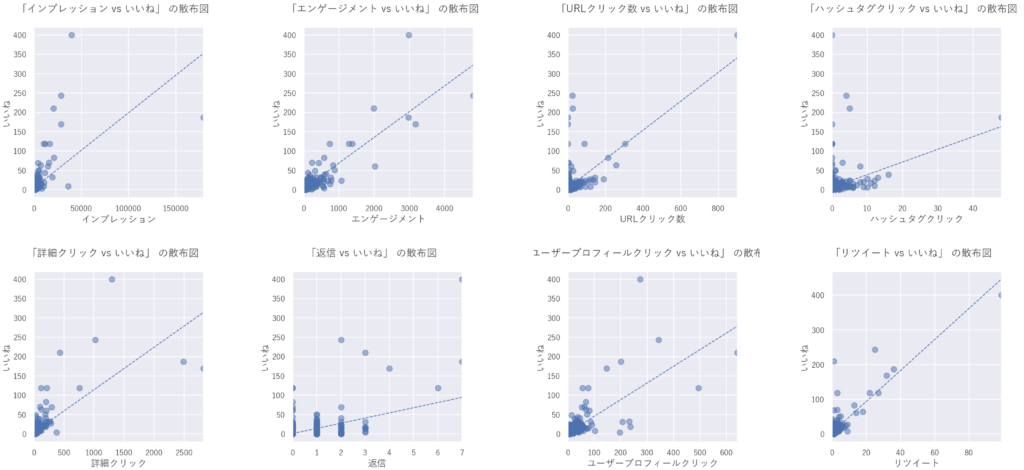
for i in df.loc[: ,"インプレッション":]:
if i != "いいね":
var_names = [i, "いいね"]
scatter_plot(df[i], df["いいね"], var_names)
「いいね」と各変数の間に大まかに正の相関が見られました。感覚的には納得できる結果かと思います。
※回帰直線は傾向を分かり易いするために引いています。参考程度。
余談ですが、DocstringはGoogle Styleがお気に入りです。
フォロワー増加数を紐付ける
「説明変数$X$が〇〇増えるツイートをすると、フォロワーが1人増える」を調べるためには、目的変数にフォロワー増加数が必要です。
以下のスクリプトでフォロワー増加数と各変数の1カ月ごとの値をデータフレームに格納します。
# socialdogsから取得した、2020/4~2021/3、2021/9~12021/11 月ごとのフォロワー増加数
fav_list = [10,70,35,20,28,28,37,141,35,113,239,127,31,52,26]
# 月ごとの合計値を出す(計量値以外はカウント)
df_sum = df.resample('M').sum()
df_count = df.resample('M').count()
# 2020/4~2021/3、2021/9~12021/11のデータだけ取り出す
df_sum = pd.concat([df_sum[:12],df_sum[-3:]],axis=0)
df_sum["フォロワー増加数"] = fav_list
df_sum["ツイート数"] = df_count["ツイート本文"]
df_sum
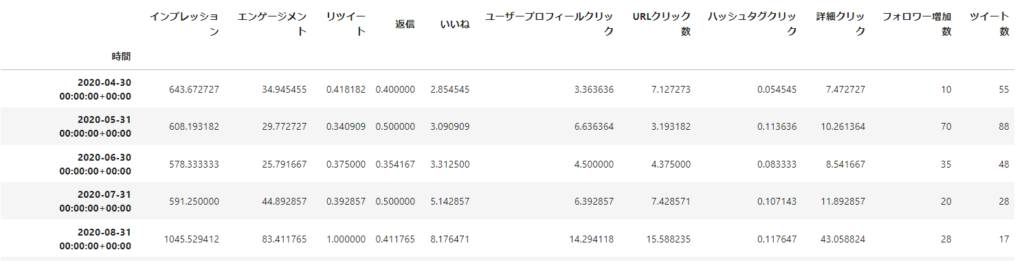
説明変数を1ツイートあたりに変換する
「説明変数$X$が〇〇増えるツイートをすると、フォロワーが1人増える」という指標を知りたいので、各変数をツイート数で割って1ツイートあたりに変換します。注意点は、「フォロワー増加数は割らない」ということです。理由は回帰分析のパートで説明します。
(勿論、ツイート数も割りません)
#1ツイート当たりに直すしたデータフレームを作成する
df_sum_pertweet = df_sum.copy()
for col in df_sum:
if (col != "フォロワー増加数" and col != "ツイート数"):
df_sum_pertweet[col] = df_sum_pertweet[col]/df_sum_pertweet["ツイート数"]
df_sum_pertweetこれで統計モデルを作成する準備が整いました。
統計モデルを作成する
どんなモデルを作るか、それが問題だ
初めに、どんなモデルを作るか? ≒ フォロワー増加数がどのような確率分布に従うか? にあたりを付ける必要があります。その方法は、以下サイトを参考にさせていただきました。
上記サイトで述べられている、以下ステップに従って、フォロワー増加数の統計モデルを作っていきます。
- 早見表・改で当たりをつける
- 目的変数の分布をヒストグラムから確認する
- 目的変数の平均値とサンプルサイズのデータを元に候補となる分布のシミュレーションを行ってみて、目的変数のヒストグラムと比較して、改めて最適な分布を定める
- 残差平方和、AIC、そしてover-dispersion検定を行って、最適と定めた分布が実際に最適か否かを判定する
出典:渋谷駅前で働くデータサイエンティストのブログ
「使い分け」ではなく「妥当かどうか」が大事:重回帰分析&一般化線形モデル選択まわりの再まとめ
1.早見表・改で当たりをつける
早見表とは、上記サイトで述べられている、参考資料1を基に作られた以下の表です。
(*):中心極限定理が効き始める程度に大きいという意味 出典:渋谷駅前で働くデータサイエンティストのブログ
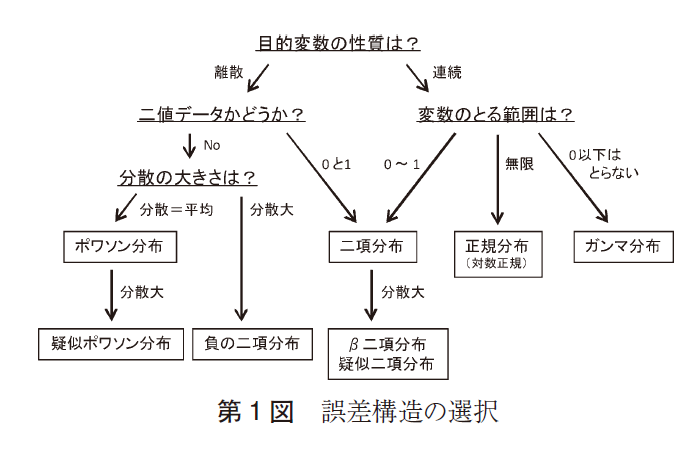
また、参考文献4には以下の参考になる図が載っていました。
上記の図表を鑑みると、フォロワー増加数は以下のいずれかの確率分布に従う可能性がありそうです。
確率分布の候補
- ポアソン分布
- 負の二項分布
(※フォロワー増加数が負に分布することはないので、正規分布は外しました)
2.目的変数の分布をヒストグラムから確認する
3.分布のシミュレーションを行ってみて、最適な分布を定める
2、3を以下で同時に検討します。
フォロワー増加数のヒストグラムと、ポアソン分布、負の二項分布の理論値を描いて、重なるか確認します。
def hist_plot(values, bins=None, x_lim=None, xlabel=None, ylabel=None, title=None, PD=False):
"""散布図を描く関数
Args:
values(pandas.Series) :変数
bins :区間数
x_lim :x軸の範囲
xlabel :x軸のラベル
ylabel :y軸のラベル
title :グラフタイトル
PD :ポアソン分布の理論曲線を描くか否か
Returns: None
"""
fig, ax = plt.subplots(figsize=(10,4), dpi=150)
ax.hist(values, bins=bins, density=True, align="left", label="確率密度")
ax.set_xlabel(xlabel,fontsize=12)
ax.set_ylabel(ylabel,fontsize=12)
ax.tick_params(axis='x', labelsize=10)
ax.tick_params(axis='y', labelsize=10)
ax.set_xlim([0, x_lim])
fig.suptitle(title, fontsize=13)
if PD == True:
x = [i for i in range(int(values.max())+5)]
ax.plot(x, poisson.pmf(x, mu=values.mean()), marker="o", color="red", markersize=4, linewidth=1, label="ポアソン分布の確率密度")
ax.legend()
bins = int(np.log2(len(df_sum))+1) # スタージェスの公式
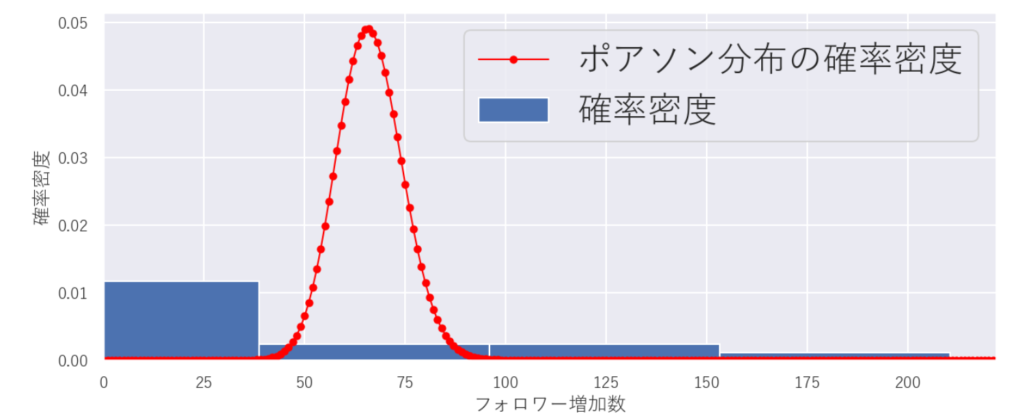
hist_plot(df_sum["フォロワー増加数"], bins, None, "フォロワー増加数", "確率密度", "フォロワー増加数の分布", True)
「強度λ = フォロワー増加数の平均」としたポアソン分布の理論曲線からかなり外れました😅
実際、ポアソン分布に従うのであれば、分散=平均になるはずです.。しかし、フォロワー増加数の平均と分散を求めてみると、かなり分散が大きい(=過分散)ことが分かります。
- フォロワー増加数の平均:66
- フォロワー増加数の分散:3959
負の二項分布についても色々パラメータを変えて、描いてみましたがヒストグラムと上手く重なりませんでした。
4.残差平方和、AIC、over-dispersion検定を行って、最適と定めた分布が実際に最適か否かを判定する
3までで、適切な確率分布が判断できませんでしたが、モデリングを進めてみます。
ここらからは、PythonではなくRを使います。統計モデリングは何かとRの方が便利なので🙄
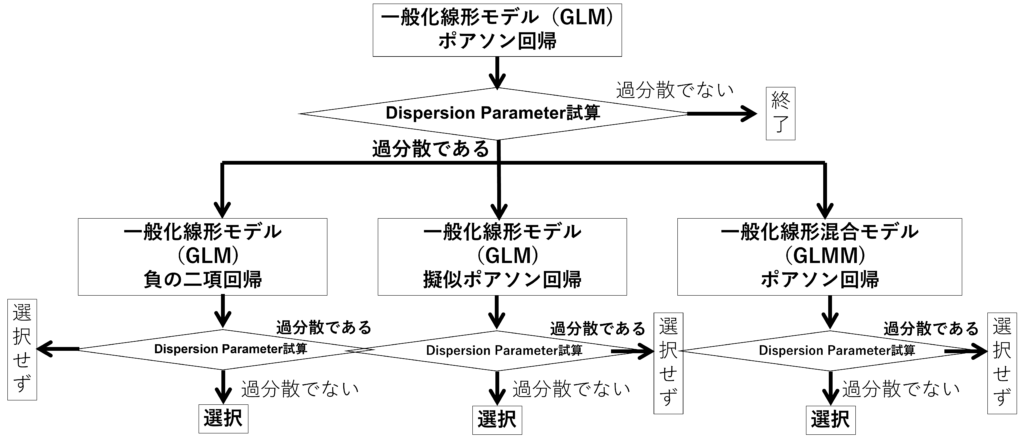
可能性のある分布は、ポアソン分布、負の二項分布なので、以下のフローに則りモデリングを進めます。モデリング後にDispersion Parameterを計算し、仮定している分布から想定される分散とモデルから試算される分散が近しいか確認します。この値が、理論値より大きいと過分散が疑われ、想定しているモデルが適切でないと判断します。
どのくらい、ずれていると不適切か?といった絶対的な指標はないそうです。。
確認しよう、過分散! ~ Dispersion Parameter ~
バラツキを表すパラメータで、分布によって値が決められています。
| 分布 | 正規分布 | ポアソン分布 | 負の二項分布 |
| Dispersion Parameter | 分散に等しい | 1 | 1 |
以下の式で計算します。
$$\frac{ピアソンのカイ二乗}{残差の自由度} = \frac{\sum\frac{(観測値-推定値)^{2}}{推定値}}{残差の自由度}$$
過分散が発生していると、本来のばらつきを過少評価していることになり、第一種の過誤(本来、有意差の無い事象を ”有意差あり” と判断してしまうこと)が起きやすくなります。
割算値の統計モデリングはやめよう!
繰り返しになりますが、今回の分析で求めたいのは、「説明変数$X$が〇〇増えるツイートをすると、フォロワーが1人増える」ということです。なので、ともすればフォロワー増加数をツイート数で割った値を目的変数にしたくなります。(実際、私は初めそうしていました💦)
しかし、参考文献2のP130 6.6に、割算値を目的変数にすることのデメリットとして、次のような記述があります。
- 情報が失われる
例えば、野球の打率で、1000打数300安打の打者と10打数3安打の打者は、どちらも同じ程度に確からしい「三割打者」と言えるでしょうか?
このように、打数・安打数という2つのデータを一つにまとめることで確からしさの情報が失われます。- 変換された値の分布はどうなる?
分子・分母にそれぞれ誤差が入った数量どうしを割算して作られた割算値はどんな確率分布に従うでしょうか?
~以下、省略~出典:データ解析のための統計モデリング 6.6章 P130(久保 拓弥)
要は、割合にしてしまうことで、情報が落ちるし、
確率分布÷確率分布てどんな確率分布か意味不明だよね~。
ということで、よろしくないということですね。
割算値の統計モデリングを回避するために、オフセット項というものを導入します。
このような理由から、データ成形の際にフォロワー増加数だけは、ツイート数で割りませんでした。詳しくは、次のポアソン回帰のパートで説明します。
GLM ~ ポアソン回帰 ~ を実施
ポアソン回帰は以下の式で表される統計モデルです。
フォロワー増加数$y_{i}$が強度$λ_{i}$で決定されるポアソン分布に従うと仮定します。
$λ_{i}$はフォロワー増加数$y_{i}$の平均値(=期待値)です。
$p(y_{i} | λ_{i}) = \frac{λ_{i}^{y_{i}}exp(-λ_{i})}{y_{i} !}$ ・・・①
そして、強度が
$λ_{i}=exp(β_{0} + β_{1} x_{1i} + β_{2} x_{2i} + β_{3} x_{3i} + ・・・) $ ・・・②
と表されるモデルです。
$x_{1i}、 x_{2i}、 x_{3i}、、、$はある月の1ツイートあたりのインプレッション数、エンゲージメント数、リツイート数などです。ツイート数は含みません。
②式の左辺を月ごとのツイート数$T_{i}$で割ります。
$\frac{λ_{i}}{T_{i}}=exp(β_{0} + β_{1} x_{1i} + β_{2} x_{2i} + β_{3} x_{3i} + ・・・)$
移項して、
$λ_{i}=T_{i}exp(β_{0} + β_{1} x_{1i} + β_{2} x_{2i} + β_{3} x_{3i} + ・・) $
これを変形すると
$λ_{i}=exp(β_{0} + β_{1} x_{1i} + β_{2} x_{2i} + β_{3} x_{3i} + ・・・$
$+ logT_{i}) $・・・③
この$logT_{i}$には偏回帰係数$β$が掛かっていません。これをオフセット項と言います。
このようにして、フォロワー増加数$y_{i}$をツイート数$T_{i}$で割ることなく、「1ツイートあたりのフォロワー増加数」を統計モデルに含めることができます。①、③式を用いて、最尤法により定数と偏回帰係数$β_{0}、β_{1} 、 β_{2} 、 β_{3} ・・・$を決めてやれば、ポアソン回帰モデルが完成します。
Rで実行します。説明変数の選択はAIC基準でステップワイズ法で行います。
尚、エラーが出たため、データフレームのカラム名を以下のように英語表記にしました。
(Python:Pandas.DataFrame ⇒ Rのデータフレーム)
- index(年月) ⇒ idindex(年月) ⇒ id
- インプレッション ⇒ Impressions
- エンゲージメント ⇒ engagement
- リツイート ⇒ Retweet
- 返信 ⇒ reply
- いいね ⇒ good
- ユーザープロフィールクリック ⇒ user_prof.
- URLクリック数 ⇒ URL
- ハッシュタグクリック ⇒ hashtag
- 詳細クリック ⇒ details
- フォロワー増加数 ⇒ followers
- ツイート数 ⇒ tweet
AICは各モデルで共通して以下の式で算出しました。GLMに用いるglm関数とGLMMに用いるglmmMLパッケージで計算の仕方が違うため です。
$AIC = Residual deviance+2×パラメータ数$
# 必要なライブラリのインポートlibrary(MASS)
library(glmmML)
library(ggplot2)
library(tidyverse)
library(jtools)# データフレーム3を保存したCSVを読み込む
df2 <- read.csv("df_GLMM_sum3.csv")
# モデル作成
glm_poisson <- glm(followers ~ Impressions + engagement + Retweet + reply + good + user_prof. + URL + hashtag + details,
offset = log(tweet), data = df2, family = poisson)# ステップワイズでで変数選択
step.glm_poisson <- stepAIC(glm_poisson)
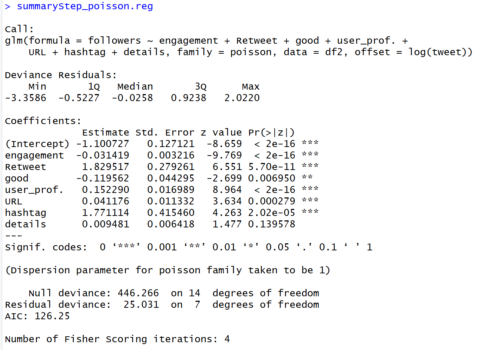
summaryStep_poisson.reg <- summary(step.glm_poisson)# AICを求める
step.glm_poisson\$deviance + 2*(step.glm_poisson\$df.residual+1)
41.03# 平方和残差を求める
sum((df2\$followers-fitted.values(step.glm_poisson ))^2)
736.22# Dispersion Parameterを求める
sum(residuals(glm_poisson, type="pearson")^2)/glm_poisson\$df.res
4.67# 決定係数を求める
step.glm_poisson.rsquared <- 1-sum(residuals(step.glm_poisson)^2)/sum((df2\$followers-mean(df$followers))^2)
0.9996
【結果】
Dispersion Parameterの理論値が1であるのに対して、モデルから推定される値は4.67です。したがって、過分散であると判断されます。
GLM ~ 負の二項回帰 ~ を実施
負の二項回帰は以下の式で表される統計モデルです。
フォロワー増加数$y_{i}$が平均$μ_{i}$ 、サイズパラメータ$θ$で決定される負の二項分布に従うと仮定します。
$$p(y_{i} | μ_{i}, θ) = \frac{\Gamma(θ+y_{i})}{\Gamma(θ)\Gamma(y_{i}+1)}(\frac{θ}{θ+μ})^{θ}(\frac{μ}{θ+μ})^{y_{i}}$$
そして、平均が
$$μ_{i}=exp(β_{0} + β_{1} x_{1i} + β_{2} x_{2i} + β_{3} x_{3i} + ・・・) $$
と表されます。
# モデル作成
model_glmnb <- glm.nb(followers ~ Impressions + engagement + Retweet + reply + good +user_prof. + URL + hashtag + details + offset(log(tweet)), data = df2)#ステップワイズでで変数選択
step.model_glmnb <- stepAIC(model_glmnb)
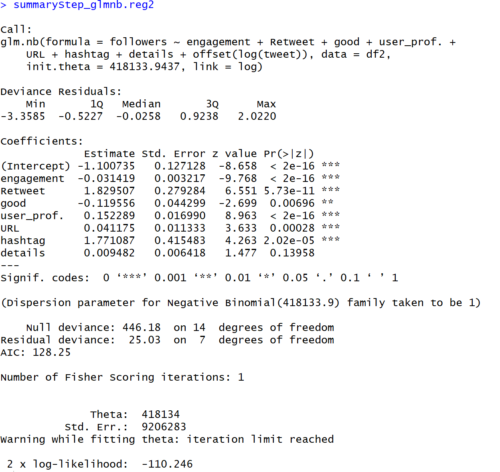
summaryStep_glmnb.reg2 <- summary(step.model_glmnb)
summaryStep_glmnb.reg2# AICを求める
step.model_glmnb\$deviance + 2*(step.model_glmnb\$df.residual+1)
41.03# 平方和残差を求める
sum((df2\$followers-fitted.values(step.model_glmnb))^2)
736.25# Dispersion Parameterを求める
sum(residuals(step.model_glmnb, type="pearson")^2)/step.model_glmnb$df.res
3.32
# 決定係数を求める
step.model_glmnb.rsquared <- 1-sum(residuals(step.model_glmnb)^2)/sum((df2\$followers-mean(df2\$followers))^2)
step.model_glmnb.rsquared
0.9996
【結果】
Dispersion Parameterの理論値が1であるのに対して、モデルから推定される値は3.32です。したがって、過分散であると判断されます。
GLM ~ 疑似ポアソン回帰 ~ を実施
疑似ポアソン分布は、ポアソン分布の分散をDispersion Parameterで重み付け、調整した確率分布です。ポアソン分布では、期待値=分散となるが、疑似ポアソン分布では、分散=$Dispersion Parameter × λ$となります。
疑似ポアソン分布では、stepAICが動かなかったため、ポアソン回帰で選択された説明変数を供用しました。
# モデル作成
glm_quasipoisson <- glm(followers ~ engagement + Retweet + good +user_prof. + URL + hashtag + details, offset = log(tweet),
data = df2, family = quasipoisson)# AICを求める
glm_quasipoisson\$deviance + 2*(glm_quasipoisson\$df.residual + 1)
41.03
# 平方和残差を求める
sum((df2\$followers-fitted.values(glm_quasipoisson))^2)
736.22# Dispersion Parameterを求める
sum(residuals(glm_quasipoisson, type="pearson")^2)/glm_quasipoisson\$df.res
3.32
# 決定係数を求める
glm_quasipoisson.rsquared <- 1-sum(residuals(glm_quasipoisson)^2)/sum((df2$followers-mean(df\$followers))^2)
glm_quasipoisson.rsquared
0.9996
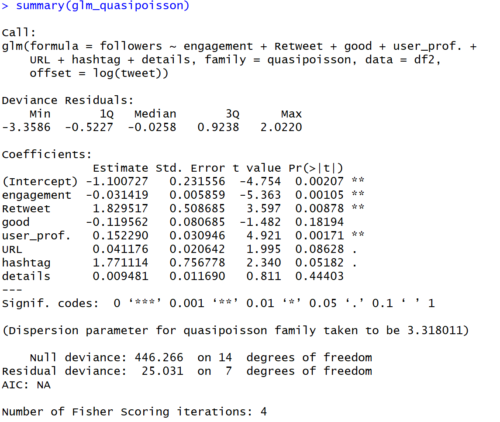
【結果】
Dispersion Parameterの理論値が3.32であるのに対して、モデルから推定される値は3.32です。したがって、過分散ではないと判断されます。
(分散を調整しているので、この表現は正しくないかも、、)
GLMM ~ ポアソン回帰 ~ を実施
最後に、一般化線形混合モデルのポアソン回帰をやってみます。
GLMでは、②式に表されるように、説明変数の値が同じであれば、フォロワー増加数の平均値($λ_{i}$)も同じという仮定を設けていました。これに対してGLMMでは、観測されていない個体差をモデルに加えます。これにより、過分散に対応しようというものです。
個体差は、説明変数で説明できない様々なばらつきの要因を含むものです。例えば、ツイートデータだと以下のようなものが想定されます。
- 年月ごとフォロワー増加数の差
(例えば、4月はフォロワーが増加しやすけど、8月は増加しにくい等。そんなこと、あるか分からないけど、、も)
個体差$r_{i}$を加えたモデルは以下になります。①、③式とほぼ変わりません。$r_{i}$が入っただけ。
$p(y_{i} | λ_{i}) = \frac{λ_{i}^{y_{i}}exp(-λ_{i})}{y_{i} !}$・・・④(①と同じ)
$λ_{i}=exp(β_{0} + β_{1} x_{1i} + β_{2} x_{2i} + β_{3} x_{3i} + ・・・$
$+ r_{i} + logT_{i}) $・・・⑤
個体差$r_{i}$はどのような確率分布に従うか分かりません。統計モデリングに便利であるという観点から平均0の正規分布を仮定します。
$p(r_{i} | s) = \frac{1}{\sqrt{2πs^{2}}}exp(\frac{r_{i}^{2}}{2s^{2}})$
$s$は個体差$r_{i}$の標準偏差です。$s$が大きいほど、個体差の大きい集団と言え、過分散になり易いと言えます。
こちらもstepAICが動かなかったため、GLMポアソン回帰で選択された説明変数を供用しました。
# モデル作成
glmm_poisson <- glmmML(followers ~ Impressions + engagement + Retweet + user_prof. + hashtag ,offset = log(tweet), data = df2, family = poisson, cluster = id, method = "ghq", start.sigma = 1)
# ※AIC、残渣平方和、Dispersion Parameterは求められなかった# 決定係数
glmm_poisson.rsquared <- 1-sum(residuals(glmm_poisson )^2)/sum((df2\$followers-mean(df2\$followers))^2)
glmm_poisson.rsquared
1
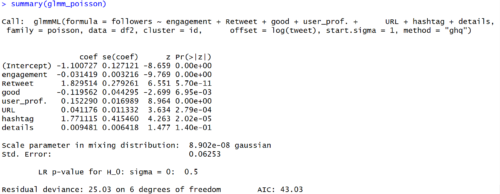
【結果】
偏回帰係数はGLMポアソン回帰、GLM疑似ポアソン回帰とほとんど変わらないです。p値が微妙に違います。注目すべきは、以下の値です。
$Scale parameter in mixing distribution:$
$sの最尤推定値 = 8.902e-08$
$Std. Error :$
$sの標準偏差 = 0.06253$
$r_{i}$がかなり小さいことから、個体差はほぼないと思われます。
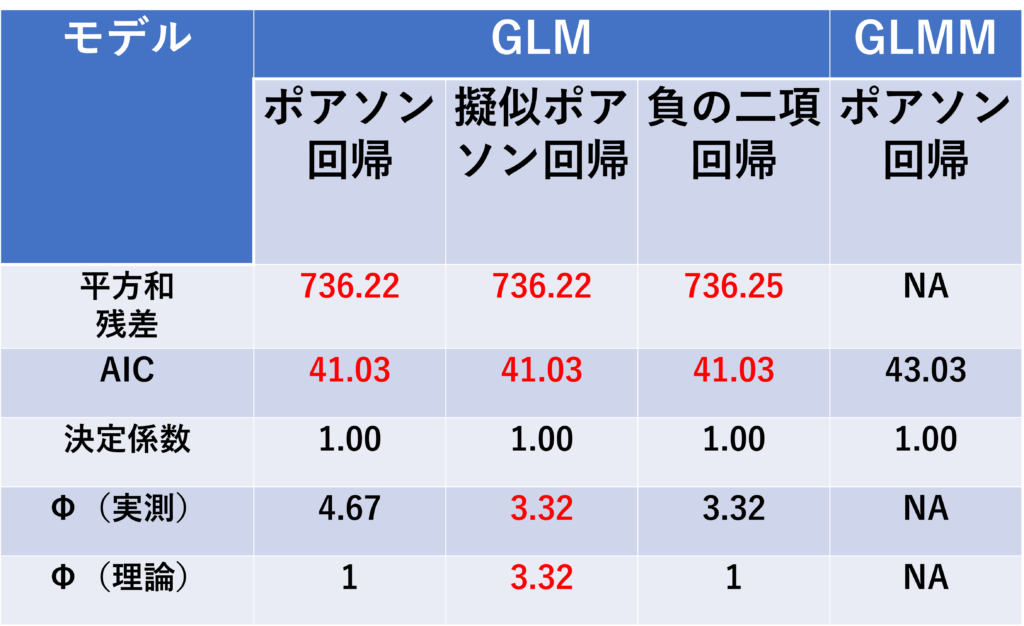
結果まとめ
以下に各モデルの平方和残差、AIC、決定係数、Dispersion Parameter$Φ$をまとめます。(※赤字はモデル選択に有利と考えられる値)
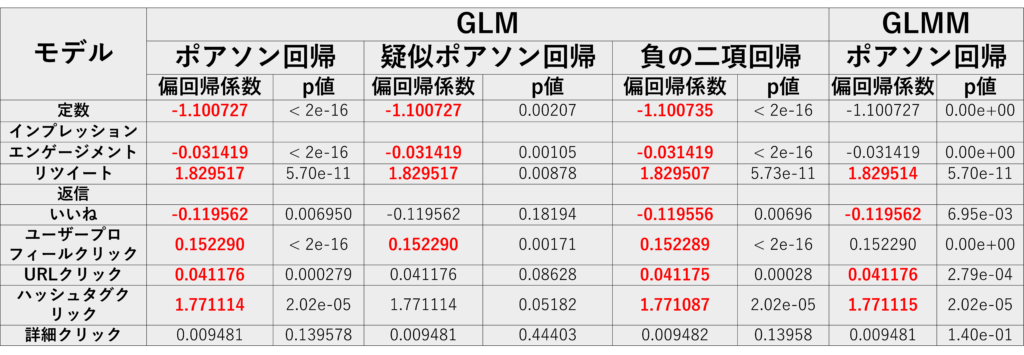
次に偏回帰係数とp値のまとめます。(※赤字は有意水準5%で有意な偏回帰係数)
以下のことが見て取れます。
- どのモデルでも(AIC基準で)選択された変数は共通
- 偏回帰係数もほとんど同じ
- 有意水準5%で有意となる変数が異なる
GLMポアソン回帰、GLM負の二項回帰で有意となる変数は共通。
一方、疑似ポアソン回帰とGLMMポアソン回帰では、有意となる変数がそれらに比べて少ない。GLMポアソン回帰、GLM負の二項回帰では、過分散のため、第一の過誤が起きやすいことを反映していると思われる。
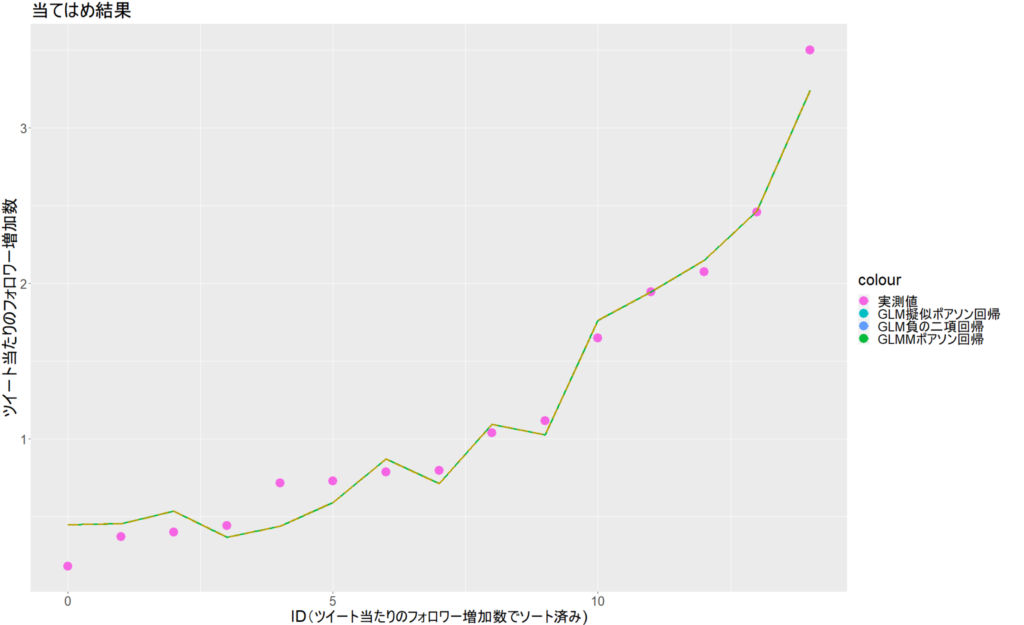
フィッティング値の可視化
上記、モデルで実測値にフィッティングした結果を図示します。
横軸の「ID」は15カ月に番号を振った番号です。ツイートあたりのフォロワー増加数でソートしています。
選択された変数と偏回帰係数がほぼ同じなので、各モデルのグラフは重なります。
# 可視化のためのデータフレームを作ります
# 各モデルの当てはめ値を計算して1つのデータフレームにまとめます
### 実測値 ###
v0 <- c(df2\$followers/df2\$tweet)
id <- c(df2\$id)
df_real <- as.data.frame(list(id, v0))
colnames(df_real) <- c("id", "Measured_value")### GLMポアソン回帰 ###
v1 <- c(fitted.values(step.glm_poisson)/df2\$tweet)
df_poisson <- as.data.frame(list(id, v1))
colnames(df_poisson) <- c("id", "glm_poisson")### GLM疑似ポアソン回帰 ###
v2 <- c(fitted.values(glm_quasipoisson)/df2\$tweet)
df_quasipoisson <- as.data.frame(list(id, v2))
colnames(df_quasipoisson) <- c("id", "glm_quasipoisson")### GLM負の二項回帰 ###
v3 <- c(fitted.values(step.model_glmnb)/df2$tweet)
df_glmnb <- as.data.frame(list(id, v3))
colnames(df_glmnb) <- c("id", "glm_nb")### GLMMポアソン回帰 ###
B0 <- glmm_poisson\$coefficients[1]
B1 <- glmm_poisson\$coefficients[2]
B2 <- glmm_poisson\$coefficients[3]
B3 <- glmm_poisson\$coefficients[4]
B4 <- glmm_poisson\$coefficients[5]
B5 <- glmm_poisson\$coefficients[6]
B6 <- glmm_poisson\$coefficients[7]
B7 <- glmm_poisson\$coefficients[8]
# 1ツイート当たりのフォロワー増加数を試算する関数
calcProb <- function(x1, x2, x3, x4, x5, x6, x7, r)
exp(B0 + B1*x1 + B2*x2 + B3*x3 + B4*x4 + B5*x5 + B6*x6 + B7*x7 + r)# $s$の上限下限を格納しておく($s$が極小なので、ほとんど意味はありません)
r_plus <- glmm_poisson$sigma
r_minus <- (-1)*glmm_poisson$sigma# $s=0$の場合(ほとんど意味はありません)
v4 <- calcProb(df2\$engagement, df2\$Retweet, df2\$good, df2\$user_prof., df2\$URL,
df2\$hashtag, df2\$details, 0)# $s=+8.902e-08$の場合(ほとんど意味はありません)
v5 <- calcProb(df2\$engagement, df2\$Retweet, df2\$good, df2\$user_prof., df2\$URL,
df2\$hashtag, df2\$details, r_plus)# $s=-8.902e-08$の場合(ほとんど意味はありません)
v6 <- calcProb(df2\$engagement, df2\$Retweet, df2\$good, df2\$user_prof., df2\$URL,
df2\$hashtag, df2\$details, r_minus)df_glmm <- as.data.frame(list(id, v4, v5, v6))
colnames(df_glmm) <- c("id", "GLMM_None", "GLMM_Plus", "GLMM_Minus")# データフレームを結合する
df_merge <- left_join(df_real, df_poisson)
df_merge <- left_join(df_merge, df_quasipoisson)
df_merge <- left_join(df_merge, df_glmnb)
df_merge <- left_join(df_merge, df_glmm)# 実測値順にソートする
df_merge <- df_merge[order(df_merge$Measured_value),]
df_merge$id <- c(seq(from=0, to=14, by=1))### 可視化 ###
g <- ggplot(NULL)
g <- g + geom_point(data = df_merge, aes(id,Measured_value, color="実測値"), size=6)
g <- g + geom_line(data = df_merge, aes(id,glm_quasipoisson, color="GLM疑似ポアソン回帰"), size=1.2)
g <- g + geom_line(data = df_merge, aes(id,glm_nb, color="GLM負の二項回帰"), size=1.2)
g <- g + geom_line(data = df_merge, aes(id,GLMM_None, color="GLMMポアソン回帰"), size=1.2)
g <- g + geom_line(data = df_merge, aes(id,GLMM_Plus, color="GLMM_ID差プラス"), size=1.2, linetype="longdash")
g <- g + geom_line(data = df_merge, aes(id,GLMM_Minus, color="GLMM_ID差マイナス"), size=1.2, linetype="longdash")
g <- g + xlab("ID(ツイート当たりのフォロワー増加数でソート済み)")
g <- g + ylab("ツイート当たりのフォロワー増加数")
g <- g + ggtitle("当てはめ結果")
g <- g + theme(text = element_text(size = 24))
g <- g + scale_color_discrete(breaks=c("実測値","GLM疑似ポアソン回帰","GLM負の二項回帰", "GLMMポアソン回帰"))
print(g)
モデルの解釈
どのモデルを採用するか、悩ましいですが、過分散の影響を調整できていると考えられるGLM疑似ポアソン回帰を採用して、結果を解釈してみます。
モデル式は以下になります。
$フォロワー増加数 =$
$exp(-1.10 -0.03×X_{1}+1.83×X_{2} -0.12×X_{3}$
$ +0.15×X_{4}+0.04×X_{5}$
$+ 1.78×X_{6}+0.01×X_{7} $
$-1.10+logT_{i})$・・・⑥
ここで、説明変数は以下のとおりです。
$X_{1} :1ツイートあたりのエンゲージメント数$
$X_{2}:1ツイートあたりのリツイート数$
$X_{3}:1ツイートあたりのいいね数$
$X_{4}:1ツイートあたりのユーザープロフクリック数$
$X_{5}:1ツイートあたりのURLリック数$
$X_{6}:1ツイートあたりのハッシュタグクリック数$
$X_{7}:1ツイートあたりの詳細クリック数$
$T_{i}:ツイート数$
⑥式の $logT_{i}$を$exp$の外に出して、左辺に移行します。
$フォロワー増加数 =$
$T_{i}exp(-1.10 -0.03×X_{1} + 1.83×X_{2} -0.12×X_{3}$
$+0.15×X_{4} + 0.04×X_{5}$
$+ 1.78×X_{6} + 0.01×X_{7})$
$ツイートあたりのフォロワー増加数 =$
$\frac{フォロワー増加数}{T_{i}} =$
$exp(-1.10 -0.03×X_{1} + 1.83×X_{2} -0.12×X_{3}$
$+0.15×X_{4} + 0.04×X_{5}$
$+ 1.78×X_{6} + 0.01×X_{7})$・・・⑦
この⑦式が最終的に求めたかった式になります。
偏回帰係数から$X_{2}(1ツイートあたりのリツイート数)$と$X_{6}(1ツイートあたりのハッシュタグクリック数)$の影響が大きいことが分かりました。
(ただし、1ツイートあたりのハッシュタグは有意水準5%で有意でない)
上記2つの変数について、フォロワー増加数に与える影響を確認します。
- 1ツイートあたりのリツイート数が1増えた場合
$\frac{⑦式でX_{2}=1}{⑦式でX_{2}=0} = exp(1.83) = 6.2$
- 1ツイートあたりのハッシュタグクリック数が1増えた場合
$\frac{⑦式でX_{6}=1}{⑦式でX_{6}=0} = exp(1.78) = 5.9$
リツイートが1件あると、平均的にフォロワー増加数が6.2倍、ハッシュタグクリックが1件あると平均的にフォロワー増加数が5.9倍になることが分かりました。
リツイートされるツイートを目指すのが良さそうです。ハッシュタグておまけ程度に付けていましたが、侮れないですね(?)。
多重共線性の確認を忘れていた!
ここまで長々と解析してきましたが、多重共線性の有無を確認していませんでした。
本来、統計モデリングの前に確認すべきですね😅

GLM疑似ポアソン回帰モデルのVIF(分散拡大係数) を確認します。
# VIFを求める
vif(glm_quasipoisson)
一般的に VIF > 10であると、多重共線性が疑われます。
なので、上記で検討した疑似ポアソン回帰モデルでは、多重共線性が疑われます。
多重共線性が発生すると偏回帰係数の標準誤差が大きくなってしまい、真に有意な変数が選択できない可能性があります。
多重共線性への対応は主に以下の3つです。
本解析の目的は、「どのようなツイートをすれば、フォロワーが増えそうか?」を調べることです。なので、偏回帰係数の解釈が必要です。
2、3の方法では、偏回帰係数から直接的に説明変数の影響を推定することが難しくなるため、今回は1の方法を選びました。
さて、どの変数を除くか?
GLM疑似ポアソン回帰モデルで偏回帰係数が5%有意水準で有意でなかった、「いいね数、URLクリック数、ハッシュタグクリック数、詳細クリック数」を除くことにしました。
GLM ~ 疑似ポアソン回帰 ~ を実施
再度、モデルを作ります。
# モデル作成(good , URL, hashtag, details を抜いたバージョン)
glm_quasipoisson_multico <- glm(followers ~ engagement + Retweet + user_prof. , offset = log(tweet), data = df2, family = quasipoisson)# AICを求める
glm_quasipoisson_multico\$deviance + 2*(glm_quasipoisson_multico\$df.residual+1)
147.7016# 平方和残差を求める
sum((df2$followers-fitted.values(glm_quasipoisson_multico))^2)
10492.12# Dispersion Parameterを求める
sum(residuals(glm_quasipoisson_multico, type="pearson")^2)/glm_quasipoisson_multico\$df.res
10.12
# 決定係数を求める
glm_quasipoisson_multico.rsquared <- 1-sum(residuals(glm_quasipoisson_multico)^2)/sum((df2$followers-mean(df\$followers))^2)
glm_quasipoisson_multico.rsquared
0.9978# VIFを求める
vif(glm_quasipoisson_multico)
VIFがだいぶ小さくなりました。多重共線性への対応はできていそうです。
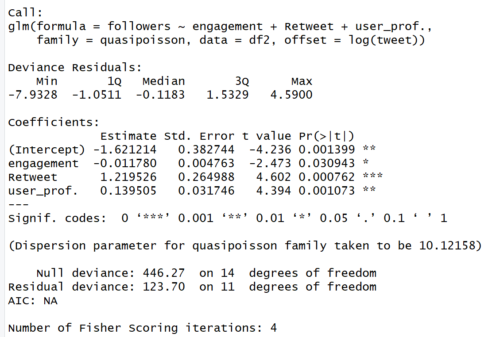
偏回帰係数を確認します。
summary(glm_quasipoisson_multico)
【結果】
全ての偏回帰係数が有意になり、またその値は対策前と変化しました。
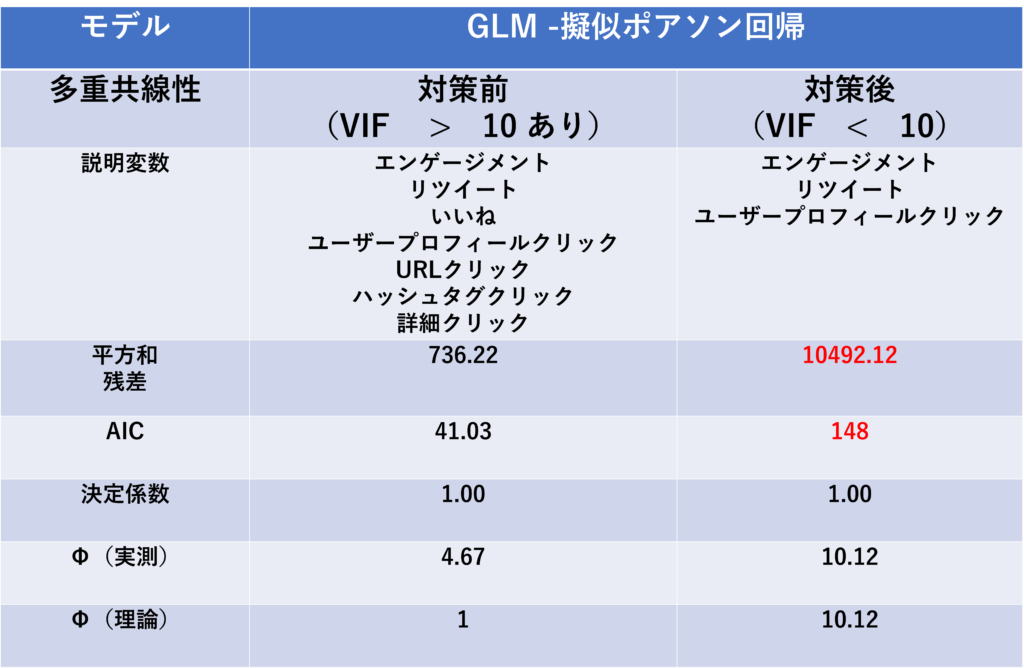
結果まとめ
多重共線性、対策前後のパラメータを比較すると以下のようになります。
変数を減らしたことで、平方和残差とAICが悪化しました。
次に偏回帰係数とp値の比較します。(※赤字は有意水準5%で有意な偏回帰係数)
リツイートの偏回帰係数とp値が対策前に比べて小さくなりました。
フィッティング値の可視化(対策前後の比較)
再度可視化します。コードは上記とほぼ同じなので、省略します。
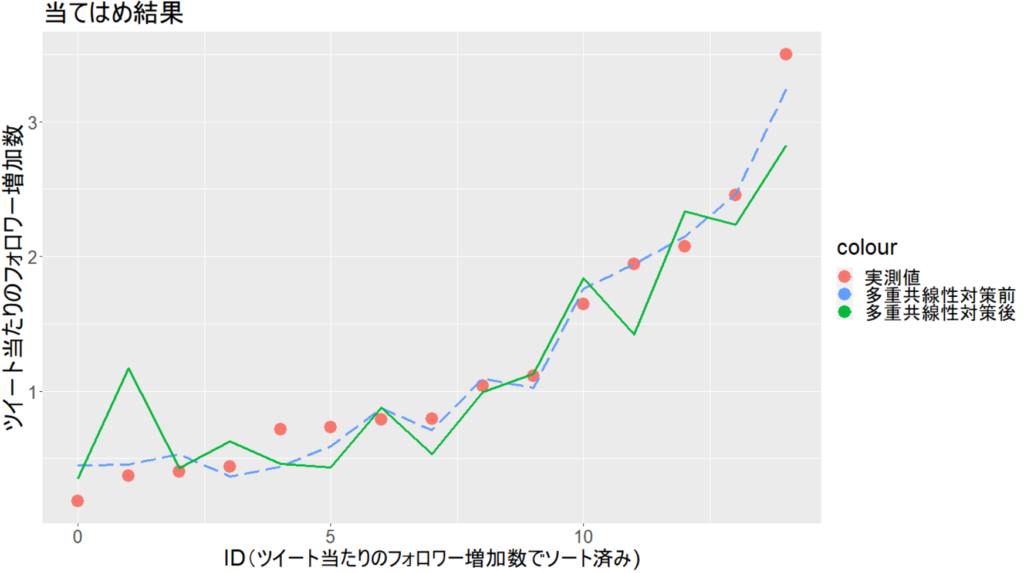
まず、フィッティング値。
多重共線性対策前に比べて、明らかに実測値との乖離が大きくなっています😅
変数を減らした影響と思われます。フォロワー増加数が小さい領域と大きい領域で特に外れています。
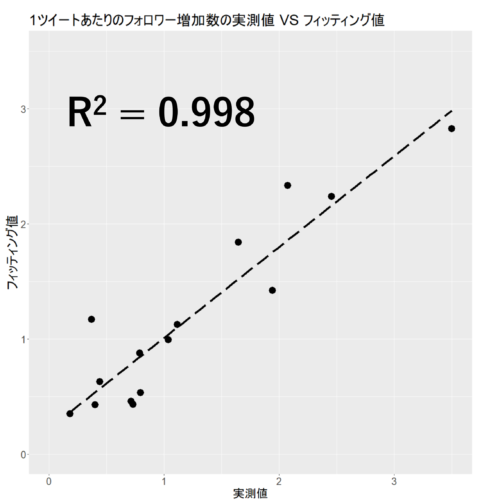
次に、1ツイートあたりのフォロワー増加数の実測値 VS フィッティング値。
明確な相関関係が見られますが、外れている点も結構あります。
モデルの解釈(多重共線性の対策後)
対策後のモデル式で、結果を解釈しなおします。
$ツイートあたりのフォロワー増加数 =$
$\frac{フォロワー増加数}{T_{i}} =$
$exp(-1.62 -0.01×X_{1}+1.22×X_{2}+0.14×X_{4})$・・・⑧
ここで、説明変数は以下のとおりです。
$X_{1} :1ツイートあたりのエンゲージメント数$
$X_{2}:1ツイートあたりのリツイート数$
$X_{4}:1ツイートあたりのユーザープロフクリック数$
$T_{i}:ツイート数$
この⑧式が最終的に求めたかった式になります。(前にも言った!)
偏回帰係数から$X_{2}(1ツイートあたりのリツイート数)$の影響が大きいことが分かります。
上記2つの変数について、フォロワー増加数に与える影響を確認します。
- 1ツイートあたりのリツイート数が1増えた場合
$\frac{⑧式でX_{2}=1}{⑧式でX_{2}=0} = exp(1.22) = 3.4$
リツイートが1件あると、平均的にフォロワー増加数が3.4倍になることが分かりました。
やはりリツイートされるツイートを目指すのが得策ぽいです!
残る問題点
今回は15カ月分(15点)のデータを使って回帰分析を実施しました。
回帰分析に必要なデータ数は色々議論があるようです。説明変数×10が目安であったり、検出力を基に決める方法などがあるようです。
いずれにせよ、今回分析したデータ数は少ない気がします。
データが少ないことによる影響は別途、調査したいと思います。
参考文献
- 北海道大学学術成果コレクション 講義のーと : データ解析のための統計モデリング(久保 拓弥)
- データ解析のための統計モデリング入門(久保 拓弥)
- 現代数理統計学の基礎(久保川達也)
- 線形モデルから一般化線形モデル(GLM)へ (大東健太郎)