2021年11月21日に統計検定1級を受験しました。
結果は以下のとおりでした。
| 科目 | 統計数理 | 統計応用 (理工学) |
| 結果 | 不合格 | 合格 |
| ランク | 不合格者の40%以下 | 成績優秀者ではない |
| 自己採点結果 | 55/100 | 55/100 |
統計数理は不合格、統計応用はギリギリ合格でした。
2022年11月20に統計数理に再挑戦する計画なので、準1級受験時と同様に、解答を作成していきます。
公式問題集は2年セットでの発売であるため、21年試験の解答が発売されるのはだいぶ先になると思われます。
本記事の内容
お断り
あくまで、自作なので正解を保証するものではありません。また、導出過程で誤りがある可能性が多分にあります。ご指摘は大歓迎ですので、よろしくお願いいたします。
はじめに
問題と略解は一般財団法人 統計質保証推進協会のサイトで公開されています。
著作権法により、無断での問題の複製・転載が禁止されているので、問題はこちらに記載しません。上のリンクから参照ください。
また、勉強、理解の都合上解答が順不同になります^_^;
問1
(1)
$E(X) = $
$\int_{0}^{\infty}xexp(-x) dx = $
$\left[-xexp(-x)\right]_0^\infty $
$+ \int_{0}^{\infty}exp(-x)dx = $ (※部分積分)
$\left[-exp(-x)\right]_0^\infty = 1$
$E(Y) = $
$\int_{0}^{1} xdx = $
$\left[\frac{1}{2}x^2\right]_0^1 = \frac{1}{2} $
(2)
$E[XY] = E[X]E[Y] = \frac{1}{2} $
(3)

$Z = X + Y , W = Y $と置く。
変数変換$(Z, W) = (u(X, Y), v(X, Y))$とし、
その逆変換を$(X, Y) = (s(Z, W), t(Z, W))$とする。
その時、$(Z, W)$の確率密度関数は、以下で表せる。
$\frac{f(s(z, w), t(z, w))}{|J(s(z, w), t(z, w))|}$・・・①
①式の分母
$|J(s(z, w), t(z, w))| = $
$\begin{vmatrix} 1 & 1 \\0 & 1 \end{vmatrix} = 1$
よって、
①式$ = f(z-w, w)$
$= f_{X}(z-w)・f_{Y}(w)$
求める、確率密度関数$f_Z(z)$は上記を$w$について積分して求める。
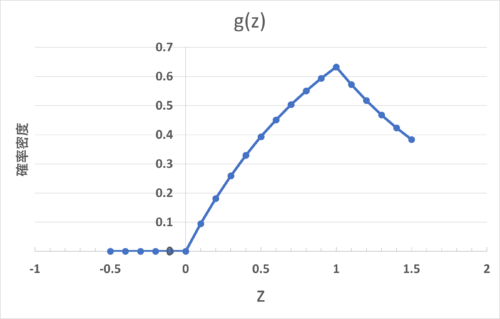
$f_Z(z) = \int_{0}^{z}exp(-(z-w)) ・f_{Y}(w)dw =$・・・②
②式を積分範囲によって場合分けして計算する。
$0<w<1$の時、$f_{Y}(w)=1$
その他の時、$f_{Y}(w)=0$
これより、
- $z<0$の時、$f_{Y}(w)=0$より、②式$=0$
- $0<z<1$の時、$f_{Y}(w)=1$より、②式$= \int_{0}^{z}exp(-(z-w))dw = 1-exp(-z)$
- $1≦z$の時、$f_{Y}(w)=0$より、②式$= \int_{0}^{1}exp(-(z-w))dw = exp(-z)(e-1)$
グラフを書くと以下のようになります。
(私は本番でグラフを書き忘れましたorz)
(4)

$f_{Y}(y)$が一様分布ということがミソですね。
命題2.19
連続型確率変数$X$の分布関数を$F_{X}(x)$とし、新たに確率変数$Y$を$Y=F_{X}(x)$で定義する。この時、$Y$の確率密度関数は$f_{Y}(y)=1$, $0<y<1$となる。これは、区間$(0,1)$の一様分布である。
この命題より、$h(x)$は$F_{X}(x)$であることが分かります。
よって、
$h(x)=F_{X}(x)=$
$= \int exp(-x) dx = -exp(-x) + C$($C$:積分定数)
$\lim_{x \to \infty} h(x) \ = 1$、 $\lim_{x \to 0} h(x) \ = 0$
より、$C=1$と求まる。
ゆえに、$h(x)=1-exp(-x)$
$E[XY]$はどうしても係数が1/2だけ合わず、解答できていません。
が、考えた途中式までを記載します。
$E[XY] = \int \int xy f_{XY}(x, y) dydx $ ・・・③
同時確率密度関数$f_{XY}(x, y)$ を求めて、③式を計算すれば良さそうです。
ベイズの定理より、
$f_{XY}(x, y) = f_{Y|X}(y|x)・f_{X}(x) =h(x)・f_{X}(x)$
$= exp(-x)-exp(-2x) $
これを③式に代入して、
$\int_{0}^{\infty} \int_{0}^{1}xy・({exp(-x)-exp(-2x)}) dydx$
$= \frac{1}{2} \int_{0}^{\infty} x ({exp(-x)-exp(-2x)}) dx$
$=-\frac{1}{2} \left[exp(-x)-\frac{1}{4}exp(-2x)\right]_0^{\infty}$ (※部分積分)
$=\frac{3}{8}$
(どうしても、略解の$\frac{3}{4}$と合いません😂
おそらく、ベイズの定理を使用した式変形が怪しいですが、解明できておりません。。)
ーーーーーーー 以下、後日記載(備忘録のため上記誤答も残す) ーーーーーーー
すうがくぶんか様で公開されている解答を確認させていただき。
上記のどこが間違っているか推測できました。
おそらく、$f_{Y|X}(y|x) = h(x)$ としている箇所が間違っていると思われます。$f_{Y|X}(y|x)$は条件付き確率密度関数ですが、と$h(x)$はXの確率分布関数であるため、条件付き確率密度ではないと思われます。。
上記解答を参考にさせていただくと以下のようになります。
$E[XY] = E[X・h(X)] = E[X・(1-exp(-X))] = $
$E[X - Xexp(-X)] = $
$E[X] - E[Xexp(-X)] = $
$1- \int_{0}^{\infty}xexp(-2x) dx = \frac{3}{4}$(部分積分)

問2
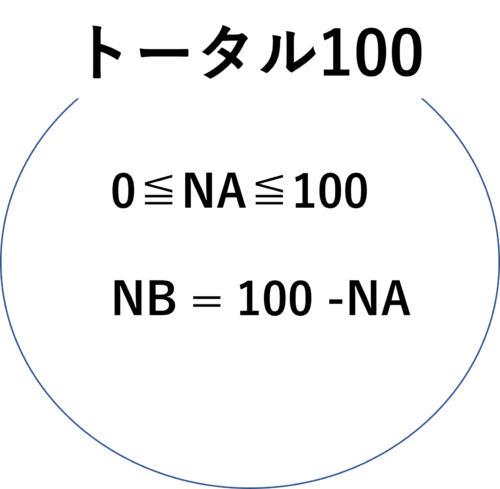
(1)
典型的な超幾何分布の問題です。
「現代数理統計学の基礎」P38 (3.9)式より、
$ \frac{\binom{N_A}{X} × \binom{100-N_A}{15-X}}{\binom{100}{15}}$・・①
①式より、
$X ≦ N_A$ かつ、$15-X ≦ 100-N_A$ であるから、
$max(0, N_A-85) ≦ X ≦min(N_A, 15)$
(2)

①式を用いて、尤度を求めます。
$L(N_A) = \frac{\binom{N_A}{4} × \binom{100-N_A}{11}}{\binom{100}{15}}$
$L(N_A+1) = \frac{\binom{N_A+1}{4} × \binom{99-N_A}{11}}{\binom{100}{15}}$
であるから、
$\frac{L(N_A+1)}{L(N_A) } = \frac{N_A-3}{N_A+1}×\frac{100-N_A}{89-N_A} < 1$
上記を満たす最小の$N_A$を求め、$N_A≒26$を得ます。

(3)

事前分布の和は1になるので、
$\sum\limits_{n=0}^{100} P(N_A=n) = C\sum\limits_{n=0}^{100} (n+1) $
$= C(\sum\limits_{n=0}^{100} n + 101) = 1$
上記を$C$について解いて、$C=\frac{1}{5151}$を得る。
(4)

ベイズの定理 $P(N_A|X) = \frac{P(N_A)×L(N_A)}{\int_{0}^{100}P(N_A)×L(N_A)dN_A}$ $P(N_A)$:事前分布 $\int_{0}^{100}P(N_A)×L(N_A)dN_A$:周辺尤度(正規化定数)
$P(N_A|X) $:事後分布
上式より、正規化定数を無視すると、
$P(N_A|X) = \frac{1}{5151}(N_A+1) × \frac{\binom{N_A}{4} × \binom{100-N_A}{11}}{\binom{100}{15}}$
$P(N_A|X)$を最大にする$N_A$を求める。
$\frac{P(N_A+1|X)}{P(N_A|X)} = \frac{N_A+2}{N_A-3}×\frac{89-N_A}{100-N_A} < 1$
上記を満たす最小の$N_A$を求め、$N_A≒30$を得ます。
問3

(1)
確率分布$P (X)$のモーメント母関数 $M_{X}(S) = E[e^{SX}] = \sum_{X}e^{SX}・P(X)$
$M_{X}(S) $:モーメント母関数
$ E[e^{SX}] = \sum\limits_{x=0}^{\infty} exp(Sx)・\frac{λ^{x}}{x!}・exp(-λ)$
$=exp(-λ)・ \sum\limits_{x=0}^{\infty} \frac{(λ・exp(S))^{x}}{x!}$
$=exp(-λ)・exp(λ・exp(S)) = exp(λ・(exp(S)-1))$

(2)
2-1
Tのモーメント母関数を求め、$P_{o}(nλ)$のモーメント母関数と等しいことを示す。
$ E[e^{ST}] = E[e^{S(X_1 + ... + X_n)}] = E[e^{S(X_1)}]・・・E[e^{S(X_n)}]$
$=(E[e^{SX}])^n = exp(nλ・(exp(S)-1))$
これは、$P_{o}(nλ)$のモーメント母関数である。ゆえに、$T ~ P_{o}(nλ)$
2-2

十分統計量 パラメータ$θ$を持つ分布から得られた標本$X_1, X_2, ,, X_n$をまとめて$X$と書くとき、以下の式を満たす統計量$T = T(X)$を$θ$の十分統計量という。 $P(X=x|T(X)=t, θ) = P(X=x|T(X)=t) $

フィッシャー・ネイマンの分解定理 $T = T(X)$が$θ$の十分統計量であるときに限り、適当な関数$h$と$g$が存在して $f(x;θ) = h(x)・g(T(x), θ)$ $f(x;θ)$:尤度
尤度を計算、変形します。
$f(x, λ) = \frac{λ^{x_1}}{x_{1}!}exp(-λ) × \frac{λ^{x_2}}{x_{2}!}exp(-λ) ×・・× \frac{λ^{x_n}}{x_{n}!}exp(-λ)$
$= \frac{1}{\prod_{i=1}^{n}x_{i}!} ・exp(-nλ)λ^T$
$=h(x)・g(T(x), λ)$
ゆえに、フィッシャー・ネイマンの分解定理より、$T$は$λ$の十分統計量である。
2-3
$f(x, λ) = \frac{1}{\prod_{i=1}^{n}x_{i}!} ・exp(-nλ)λ^T$
両辺のlogを取り、対数尤度にします。
$log(f(x, λ)) = -nλ-log(\prod_{i=1}^{n}x_{i}!) + Tlogλ$
両辺を$λ$で微分し、$0$となる$λ$を求めます。
$ \frac{\partial log(f(x, λ))}{\partial λ} = -n + \frac{T}{λ} = 0$
$\widehat{λ} = \frac{T}{n}$
(3)

2次方程式の解の公式 $ax^{2} + bx + c = 0$の解は、 $x = \frac{-b±\sqrt{b^{2}-4ac}}{2a}$
$-c ≦ \frac{T-nλ}{\sqrt{nλ}} ≦ c$
$⇔ \frac{(T-nλ)^2}{nλ} ≦ c^2$
整理して、
$n^{2}λ^{2}-(c^{2}n + 2nt)λ + T^{2} ≦ 0$
解の公式を使用して、
$\frac{2+T-2\sqrt{1+T}}{n} ≦ λ ≦ \frac{2+T+2\sqrt{1+T}}{n}$
(4)

(3)で求めた、信頼区間の中点を求めます。
$(\frac{2+T-2\sqrt{1+T}}{n} + \frac{2+T+2\sqrt{1+T}}{n}) ÷ 2 = \frac{2+T}{n}$
つまり、
$\widehat{λ} = \frac{T}{n} < \frac{2+T}{n}$
信頼区間の中点は最尤推定量よりも大きくなるため、$λ$は$\widehat{λ}$よりも大きくなる可能性が高いと言えます。

問4

多項定理 $(x_{1} + x_{2} + ・・・+ x_{k})^{n}$を展開した時の$x_{1}^{e_1} x_{2}^{e_2} ・・・x_{k}^{e_k} $の係数は、 $e_1 + e_2 + ・・・+ e_k = n$かつ$e_i ≧ 0$なら、$\frac{n!}{e_{1}!e_{2}!・・e_{k}!}$ (そうでないなら、0)
(1)
$V(\bar{X}) = V(\frac{1}{n}\sum\limits_{i=1}^{n}X_{i})$
$=\frac{1}{n^2}V(\sum\limits_{i=1}^{n}X_{i}) = \frac{1}{n^2} × nσ^2$
$= \frac{σ^2}{n} $
(2)

$E[(X_{1} - X_{2} )^3] = E[((X_{1}-μ) - (X_{2}-μ))^3]$
$=E[(X_{1} - X_{2})^3 - 3(X_{1}-μ)^{2} (X_{2}-μ) + 3(X_{1}-μ) (X_{2}-μ)^{2} - (X_{2}-μ)^{3}]$
$=E[(X_{1}-μ)^3] - 3E[(X_{1}-μ)^2]E[(X_{2}-μ)] + 3E[(X_{1}-μ)]E[(X_{2}-μ)^2] - E[(X_{2}-μ)^3]$
$=τ -3・σ^{2}・(μ-μ) +3・(μ-μ) ・σ^{2} - τ$
$=0$
(3)
超サービス問題です。
$E[Y_{i}^3] = E[(X_{i} - μ)^3] = τ$
$E[Y_{i}^{2}Y_{j}] = E[(X_{i} - μ)^2]E[(X_{j} - μ)] = σ^{2}・(μ-μ) = 0$
$E[Y_{i}Y_{j}Y_{k}] = E[(X_{i} - μ)(X_{j} - μ)(X_{k} - μ)] = (μ-μ)・(μ-μ)・(μ-μ)=0$
(4)

$\sum\limits_{i=1}^{n} (X_{i} - \bar{X})^{3} = n× (X_{1} - \bar{X})^{3}$
$ (X_{1} - \bar{X})^{3}$を求めて、最後に$n$倍します。
$ (X_{1} - \bar{X})^{3} = E[((X_{1}-μ) + (μ-\bar{X}))^{3}] $
※上記の変形は多用する
$=E[(Y_{1} - \frac{1}{n}(Y_{1} + .... +Y_{n}))^{3}]$
$=E[Y_{1}^{3}] + 3E[Y_{1}^{2} (- \frac{1}{n}(Y_{1} + .... +Y_{n}))] + 3E[Y_{1} (- \frac{1}{n^{2}}(Y_{1} + .... +Y_{n})^{2})]$
$- \frac{1}{n^{3}}E[(Y_{1} + .... +Y_{n})^{3}]$
$=E[Y_{1}^{3}] - \frac{3}{n}E[Y_{1}^{3}] + \frac{3}{n^{2}}E[Y_{1}^{3}] - \frac{1}{n^{3}}E[(Y_{1}^{3} + .... +Y_{n}^{3})] $
※(3)で求めた関係を使って、期待値が0の箇所は記載を省略している
$=τ - \frac{3}{n}τ +\frac{3}{n^{2}}τ - \frac{1}{n^{2}}τ = $
$=\frac{(n-2)(n-1)}{n^{2}}τ $
上式を$n$倍して、
$=\frac{(n-2)(n-1)}{n}τ $