本記事の内容
はじめに
製造業でデータサイエンティストをしていると、設備のセンサーデータを扱うことが多いです。 センサーデータから、設備や品質異常時の特徴を捉えて、その特徴を基に要因解析したり、生産に影響が出る前にアラートを出す取り組み(予知保全)が昨今注目されています。 今回、ある設備から1cyc(タクト毎)に出力される波形データから、正常時の波形と設備異常時の波形を区別する特徴をCNNを用いて 抽出するこを試みます。 目的は、現場のエキスパートでも分からない、機微な違いを深層学習を使って見抜くことです。 その上で、以下のいずれかの方法と取ります。
- CNNで抽出した特徴そのものを用いて、要因解析や予知保全に活用する
- CNNで抽出した特徴に着目して、別途特徴量を作成し、要因解析や予知保全に活用する
データセットの用意

close up of asian male technician in sterile coverall holds wafer that reflects many different colors with gloves and check it at semiconductor manufacturing plant
データが無ければ、何も始まりません。
まず、データセットを用意します。 本来は、実務で扱っているデータセットがおあつらえ向きですが、私的利用できないので、なるべく近いデータセットを探します。 今回使うのは、以下のデータセットです。
This dataset was formatted by R. Olszewski as part of his thesisGeneralized feature extraction for structural pattern recognition in time-series dataat Carnegie Mellon University, 2001. Wafer data relates to semi-conductor microelectronics fabrication. A collection of inline process control measurements recorded from various sensors during the processing of silicon wafers for semiconductor fabrication constitute the wafer database; each data set in the wafer database contains the measurements recorded by one sensor during the processing of one wafer by one tool. The two classes are normal and abnormal. There is a large class imbalance between normal and abnormal (10.7% of the train are abnormal, 12.1% of the test).
半導体ウエハの加工中のセンサーデータの様です。
1cycごとに”正常”、”異常"ラベルが付与されており、正常データと、異常データ数に大きな不均衡があります。
データは訓練データとテストデータの2種類があります。 これは、後ほど学習用のデータセットを作成する時に留意します。 いくつかの正常データと異常データを以下の示します。波形のどの部分に着目すれば、正常/異常を見分けられるか分かりますでしょうか?(このデータセットは結構分かり易いですが、実際の製造工程から出力されるデータは、人の目で見分けることが難しいことも多々あります。
<正常波形 例>
<異常波形 例>
モデル構築の前提
以下をモデル構築の前提とします。
- 波形データの一定時間幅での特徴を捉えられるCNNを用いる
- 特徴を理解し易くするために、畳込み後に時点数が減らない様、 カーネルサイズ、パディング、ストライドを設定する
今回は、152時点の1次元のデータに対して3層の畳み込み層を持つ、CNNを使用しました。
各畳み込み層で畳み込んだ後で、時点数が減らない様に、カーネルサイズ、パディング、ストライドを設定しています。 各畳み込み層の間にはReLU活性化関数を噛ましています。
また、時系列情報(データ挙動の前後関係)を損なわないために画像分類モデルの出力層付近によく見られるglobal average pooling層は 設けていません。
$O = \frac{I+2P-K}{S}+1$
ここで、
$O=出力データ長$
$I=入力データ長$
$P=パディングサイズ$
$K=カーネルサイズ$
$S=ストライドサイズ$
です。
上記式を、今回使用するデータに当てはめると以下となり、出力データ長と入力データ長が各畳み込み層で一致することが分かります。
$152 = \frac{152+2×7-15}{1}+1$
分類に寄与している時点をどう特定するか
正常波形と異常波形の分類精度が十分に高い場合、CNNが波形のどこに着目して分類しているか(=波形のどの部位が異常、正常たらしめているか?)を 確認します。
今回用いた方法は、深層学習 改訂第2版 (機械学習プロフェッショナルシリーズ) P195 9.2章に着想を得て、微分を用いる方法を使いました。
https://books.rakuten.co.jp/rb/16963763/
実務で使用する際は、異常データ、正常データごとの「傾向」が把握できれば良いので以下の様に平均値を取って可視化します。
更に、元々の入力データの変動(標準偏差)が大きい時点は、分類に効いていると考えられるため(逆に全データと通して、変動していない時点は分類に 影響しようなない)、入力データの標準偏差を掛けておきます。
また、正常データと異常データでは、分類に寄与している時点が異なるため、正常データと異常データを分けて寄与度を計算します。
具体的には以下の式になります。
正常データの$i$時点の分類寄与度
$d(normal)_{i}$
$= \frac{1}{n} \sum_{k=1}^{n} \frac{\partial loss_{k}}{\partial x_{k,i}}×std(x_{i})$・・・①
異常データの$i$時点の分類寄与度
$d(anomaly)_{i}$
$= \frac{1}{m} \sum_{k=1}^{m} \frac{\partial loss_{k}}{\partial x_{k,i}}×std(x_{i})$・・・②
$ std$は標準偏差を表します。
ここで、
$n=正常データ数$
$m=異常データ数$
$d(normal)_{i}=正常データのi時点の分類寄与度$
$d(anomaly)_{i}=正常データのi時点の分類寄与度$
$loss_{k}=k個目の波形に対する損失$
$x_{k,i}=k個目の入力データのi時点の値$
$std(x_{i})=入力データのi時点の値の標準偏差$
です。
$d(normal)_{i} , d(anomaly)_{i} $の意味を簡単に表現すると、入力波形のi時点の値が変化した時に、損失がどの程度変化するか?ということを表しています。
つまり、$d(normal)_{i} , d(anomaly)_{i} $の絶対値が大きい時点は分類(正常 or 異常)精度への影響が大きいと言えます。
さらに、この分類寄与度の利点は各時点の値がどちらに動けば(増加 or 減少)、正常波形、異常波形に近づくか分かることです。
①、②式から以下のことが分かります。
$d(normal)_{i} > 0$の領域 ⇒ $i$時点の値が減ると「正常波形」に近づく
$d(normal)_{i} < 0$の領域 ⇒ $i$時点の値が増えると「正常波形」に近づく
$d(anomaly)_{i} > 0$の領域 ⇒ $i$値が減ると「異常波形」に近づく
$d(anomaly)_{i} < 0$の領域 ⇒ $i$値が増えると「異常波形」に近づく
分類寄与度の符号と、値の増減の関係が逆になることに注意が必要です。
データセットを使ってトライ!

1.データローダーを作成する
それでは、前述のデータセットを使って分類寄与度を算出してみます。 CNNのモデル作成には、PyTorchを使います。なお、以下のコードは、Google ColabのランタイムをGPU設定にして動かすことを前提としています。
# 必要なライブラリのインポート
import torch
from torch import nn
from torch.nn import functional as F
from torch.utils.data import DataLoader
from torch.utils.data import random_split
from torchvision import transforms
from tqdm import tqdm
import numpy as np
import pandas as pd
from sklearn.metrics import f1_score
from sklearn.metrics import accuracy_score
from sklearn.metrics import matthews_corrcoef
from sklearn.metrics import roc_auc_score
import matplotlib.pyplot as plt
import seaborn as sns
import glob
from collections import Counter
from sklearn.datasets import make_classification
from imblearn.over_sampling import SMOTE
from imblearn.under_sampling import RandomUnderSampler
# scipy.statsから、 poissonをインポートします
from scipy.stats import poisson, nbinom
import scipy.stats
from statsmodels.sandbox.regression.predstd import wls_prediction_std
from decimal import Decimal, ROUND_HALF_UP, ROUND_HALF_EVEN
import statsmodels.api as sm
from statistics import mean
sns.set(font_scale=2)
from functools import partial
#最大表示列数の指定(ここでは50列を指定)
pd.set_option('display.max_columns', 50)
pd.set_option('display.max_rows', 50)
from sklearn.metrics import r2_score# ドライブをマウントする
from google.colab import drive
drive.mount('/content/drive')
# カレントディレクトリを変更
%cd "/content/drive/MyDrive/Wafer"
# データパスの設定
train_path = r"/content/drive/MyDrive/Wafer/Wafer_TRAIN.xlsx" # 訓練データ
test_path = r"/content/drive/MyDrive/Wafer/Wafer_TEST.xlsx" # テストデータ
# データの読み込み
df_train = pd.read_excel(train_path, header=None) # 訓練データ
df_test = pd.read_excel(test_path, header=None) # テストデータ
display(df_train.head())0列目は正常(1)、異常(-1)ラベルです。1~152列目が各時点の値になります。
# ラベル列(0)を1 ⇒ 0,-1 ⇒ 1に置き換える
df_train = df_train.replace({0: {1:0, -1: 1}})
df_test = df_test.replace({0: {1:0, -1: 1}})
# 訓練データに含まれる異常データと正常データの個数を比較する
print("正常データ数:", len(df_train[df_train[0]==0])) # 正常データ数: 903
print("異常データ数:", len(df_train[df_train[0]==1])) # 異常データ数: 97
# テストデータに含まれる異常データと正常データの個数を比較する
print("正常データ数:", len(df_test[df_test[0]==0])) # 正常データ数: 5499
print("異常データ数:", len(df_test[df_test[0]==1])) # 異常データ数: 665
# 訓練データとテストデータを結合する(後で、訓練、検証、テストに分けます)
df_train = pd.concat([df_train, df_test], axis=0)
#データを説明変数と目的変数に分ける
train_data = df_train.drop(0,axis=1)
train_target = df_train.iloc[:,0]
#データ数の確認
print(train_data.shape) # (7164, 152)
print(train_target.shape) # (7164,)次にデータ前処理として、標準化を行います。ニューラルネットを利用する場合、基本的に標準化をしておく必要があります。 ここで、1次元の時系列データの標準化方法は3つあります。
- 全波形、全時点のデータの平均、標準偏差を使って標準化する
- 時点毎に標準化する
- 値毎に標準化する
畳み込みによる特徴量抽出では、時系列情報(データ挙動の前後関係)が保たれていることが重要になります。そのため、各時点の値の大小関係が崩れない1の方法を選択しました。
# データの標準化
train_data = pd.DataFrame(scipy.stats.zscore(train_data.values, axis=None)) #全データを使って標準化する
# tensor形式へ変換
all_data = torch.tensor(train_data.values, dtype=torch.float32)
all_target = torch.tensor(train_target.values, dtype=torch.int64)
# 目的変数と入力変数をまとめてdatasetに変換
all_dataset = torch.utils.data.TensorDataset(all_data, all_target)
# 訓練、検証、テストデータへ分割する
# train : val : test = 60% : 20% : 20%
n_train = int(len(all_dataset) * 0.6)
n_val = int((len(all_dataset) - n_train) * 0.5)
n_test = len(all_dataset) - n_train - n_val
# データ数を確認する
print(n_train) # 4298
print(n_val) # 1433
print(n_test) # 1433
# データセットを分割する
torch.manual_seed(0) #乱数を与えて固定
train, val, test = torch.utils.data.random_split(all_dataset, [n_train, n_val,n_test])次にデータローダーを作成します。 この際のポイントは、正常データ数と、異常データ数を均衡させて訓練データのローダーを作成することです。 訓練データのローダー内の正常データ数と異常データ数に不均衡がある場合、多い方の分類に過学習したモデルが作製されてしまいます。
device1 = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 正常データの入力データ、ラベル格納用リスト
normal_inputs = []
normal_labels = []
# 異常データの入力データ、ラベル格納用リスト
anomaly_inputs = []
anomaly_labels = []
# 訓練データローダーの作成
train_loader = torch.utils.data.DataLoader(train , batch_size=n_train, shuffle=False)
# 正常データと異常データを分ける
for batch in train_loader:
inputs, labels = batch
inputs = inputs.to(device1)
labels = labels.to(device1)
for i in range(len(labels)):
if labels[i] == 0:
normal_inputs.append(inputs[i].to('cpu').detach().numpy().copy())
normal_labels.append(labels[i].to('cpu').detach().numpy().copy())
else:
anomaly_inputs.append(inputs[i].to('cpu').detach().numpy().copy())
anomaly_labels.append(labels[i].to('cpu').detach().numpy().copy())
# ndarrayへの変換
normal_inputs = np.array(normal_inputs)
normal_labels = np.array(normal_labels)
anomaly_inputs = np.array(anomaly_inputs)
anomaly_labels = np.array(anomaly_labels)
# tensor形式へ変換
normal_data = torch.tensor(normal_inputs, dtype=torch.float32)
normal_target = torch.tensor(normal_labels, dtype=torch.int64)
anomaly_data = torch.tensor(anomaly_inputs, dtype=torch.float32)
anomaly_target = torch.tensor(anomaly_labels, dtype=torch.int64)
# 目的変数と入力変数をまとめてdatasetに変換
normal_dataset = torch.utils.data.TensorDataset(normal_data, normal_target)
anomaly_dataset = torch.utils.data.TensorDataset(anomaly_data, anomaly_target)
# バッチサイズの設定
normal_train_batch_size = 200
anomaly_train_batch_size = 200
# 正常データと異常データ別に訓練ローダー作成
normal_train_loader = torch.utils.data.DataLoader(normal_dataset, batch_size=normal_train_batch_size, shuffle=True,drop_last=True)
anomaly_train_loader = torch.utils.data.DataLoader(anomaly_dataset, batch_size=anomaly_train_batch_size, shuffle=True,drop_last=True)
print(len(normal_train_loader.dataset)) #3834
print(len(anomaly_train_loader.dataset)) #464torch.utils.data.DataLoader(normal_dataset, batch_size=200, shuffle=True,drop_last=True)において、drop_last=Trueを指定している点がポイントです。 この様にすることで、1エポック内の正常データ数と異常データ数を均衡させて学習することができます。 次に検証データローダーを作成します。
val_loader = torch.utils.data.DataLoader(val , batch_size=n_val, shuffle=False)
device1 = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
normal_inputs = []
normal_labels = []
anomaly_inputs = []
anomaly_labels = []
# 正常データと異常データ数の確認
for batch in val_loader:
inputs, labels = batch
inputs = inputs.to(device1)
labels = labels.to(device1)
for i in range(len(labels)):
if labels[i] == 0:
normal_inputs.append(inputs[i].to('cpu').detach().numpy().copy())
normal_labels.append(labels[i].to('cpu').detach().numpy().copy())
else:
anomaly_inputs.append(inputs[i].to('cpu').detach().numpy().copy())
anomaly_labels.append(labels[i].to('cpu').detach().numpy().copy())
print(len(normal_labels)) #1285
print(len(anomaly_labels)) #148最後にテストデータローダーを作成します。
test_loader = torch.utils.data.DataLoader(test , batch_size=n_test, shuffle=False)
device1 = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
normal_inputs = []
normal_labels = []
anomaly_inputs = []
anomaly_labels = []
# 正常データと異常データ数の確認
for batch in test_loader:
inputs, labels = batch
inputs = inputs.to(device1)
labels = labels.to(device1)
for i in range(len(labels)):
if labels[i] == 0:
normal_inputs.append(inputs[i].to('cpu').detach().numpy().copy())
normal_labels.append(labels[i].to('cpu').detach().numpy().copy())
else:
anomaly_inputs.append(inputs[i].to('cpu').detach().numpy().copy())
anomaly_labels.append(labels[i].to('cpu').detach().numpy().copy())
print(len(normal_labels)) #1283
print(len(anomaly_labels)) #1502.CNNを定義する
次にCNNモデルを定義します。モデルは、Google Colabノードブックではなく、CNN_model.pyというファイルを作り、その中に記載することにします。
# CNN_model.pyの中身
from torch import nn
from torch.nn import functional as F
class Net(nn.Module):
# 使用するオブジェクトを定義
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv1d(1, 64, kernel_size=15, padding=7, stride=1)
self.conv2 = nn.Conv1d(64, 128, kernel_size=15, padding=7, stride=1)
self.conv3 = nn.Conv1d(128, 128, kernel_size=15, padding=7, stride=1)
# 順伝播
def forward(self, x):
x = x.unsqueeze(1)
x = self.conv1(x)
x = F.relu(x)
x = self.conv2(x)
x = F.relu(x)
x = self.conv3(x)
return x
class Decoder(nn.Module):
def __init__(self):
super(Decoder, self).__init__()
self.fc1 = nn.Linear(152*128,1)
# 順伝播
def forward(self, x):
#x = self.gap(x)
x = x.view(x.size(0),-1)
x = self.fc1(x)
return x
class Autoencoder(nn.Module):
def __init__(self):
super(Autoencoder, self).__init__()
self.enc = Net()
self.dec = Decoder()
# 順伝播
def forward(self, x):
x = self.enc(x)
x = self.dec(x)
return x# 上記モデルをインポートします
from CNN_model import Net, Decoder, Autoencoder3.学習を実行する
次に学習用の関数を定義します。 エポックごとにloss、accuracy,、F1-Score、Matthews Correlation Coefficientを可視化する関数も同時に定義しています。
def train_model(net, criterion, normal_train_loader, anomaly_train_loader, val_loader, optimizer, num_epoch):
#入れ子を用意(各lossとaccuracy, F1-Score、 Matthews Correlation Coefficientを入れていく)
l= []
a =[]
f1 =[]
mcc =[]
# ベストなネットワークの重みを保持する変数
best_acc = 0.0
# GPUが使えるのであればGPUを有効化する
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
net = net.to(device)
# (エポック)回分のループ
for epoch in range(num_epoch):
print('Epoch {}/{}'.format(epoch + 1, num_epoch))
print('-'*20)
for phase in ['train', 'val']:
if phase == 'train':
# 学習モード
net.train()
else:
# 推論モード
net.eval()
epoch_loss = 0.0
epoch_corrects = 0
# 学習
if phase == 'train':
for (inputs_normal, labels_normal), (inputs_anormaly, labels_anormaly) in zip(normal_train_loader, anomaly_train_loader):
inputs = torch.cat([inputs_normal, inputs_anormaly], dim=0)
labels = torch.cat([labels_normal, labels_anormaly], dim=0)
inputs = inputs.to(device)
labels = labels.to(device)
# 勾配を初期化する
optimizer.zero_grad()
# 学習モードの場合のみ勾配の計算を可能にする
with torch.set_grad_enabled(phase == 'train'):
outputs = net(inputs)
m = nn.Sigmoid() #追加
preds = torch.round(m(outputs)) #追加
# 損失関数を使って損失を計算する
labels = labels.view(-1, 1) #追加
loss = criterion(outputs, labels.to(torch.float32)) #追加
if phase == 'train':
# 誤差を逆伝搬する
loss.backward()
# パラメータを更新する
optimizer.step()
epoch_loss += loss.item() * inputs.size(0)
epoch_corrects += torch.sum(preds == labels.data)
if phase == 'val':
for inputs, labels in tqdm(val_loader):
inputs = inputs.to(device)
labels = labels.to(device)
# 勾配を初期化する
optimizer.zero_grad()
# 学習モードの場合のみ勾配の計算を可能にする
with torch.set_grad_enabled(phase == 'train'):
outputs = net(inputs)
m = nn.Sigmoid()
preds = torch.round(m(outputs))
# 損失関数を使って損失を計算する
labels = labels.view(-1, 1)
loss = criterion(outputs, labels.to(torch.float32))
epoch_loss += loss.item() * inputs.size(0)
epoch_corrects += torch.sum(preds == labels.data)
if phase == 'train':
if len(normal_train_loader) > len(anomaly_train_loader):
# 1エポックでの損失を計算
epoch_loss = epoch_loss / (len(labels)*len(anomaly_train_loader))
# 1エポックでの正解率を計算
epoch_acc = epoch_corrects.double() / (len(labels)*len(anomaly_train_loader))
else:
# 1エポックでの損失を計算
epoch_loss = epoch_loss / (len(labels)*len(normal_train_loader))
# 1エポックでの正解率を計算
epoch_acc = epoch_corrects.double() / (len(labels)*len(normal_train_loader))
if phase == 'val':
# 1エポックでの損失を計算
epoch_loss = epoch_loss / len(val_loader.dataset)
# 1エポックでの正解率を計算
epoch_acc = epoch_corrects.double() / len(val_loader.dataset)
# 1エポックでのF1-Scoreを計算
epoch_f1 = f1_score(preds.to('cpu').detach().numpy().copy(), labels.to('cpu').detach().numpy().copy())
# 1エポックでのMCCを計算
epoch_mcc = matthews_corrcoef(preds.to('cpu').detach().numpy().copy(), labels.to('cpu').detach().numpy().copy())
print('{} Loss: {:.4f} Acc: {:.4f} F1: {:.4f} MCC: {:.4f}'.format(phase, epoch_loss, epoch_acc, epoch_f1, epoch_mcc))
#lossとaccをデータで保存する
a_loss = np.array(epoch_loss)
a_acc = np.array(epoch_acc.cpu()) # GPU⇒CPUに変換
a_f1 = np.array(epoch_f1)
a_mcc = np.array(epoch_mcc)
a.append(a_acc)
l.append(a_loss)
f1.append(a_f1)
mcc.append(a_mcc)
# 一番良い精度の時にモデルデータを保存
if phase == 'val' and epoch_acc > best_acc:
# best_accを更新
best_acc = epoch_acc
print('save model epoch:{:.0f} loss:{:.4f} acc:{:.4f}'.format(epoch,epoch_loss,epoch_acc))
torch.save(net.state_dict(), 'best_model.pth')
#testとvalのlossとaccを抜き出してデータフレーム化
a_train = a[::2]
l_train = l[::2]
f1_train = f1[::2]
mcc_train = mcc[::2]
a_train = pd.DataFrame({'train_acc':a_train})
l_train = pd.DataFrame({'train_loss':l_train})
f1_train = pd.DataFrame({'train_f1':f1_train})
mcc_train = pd.DataFrame({'train_mcc':mcc_train})
a_val = a[1::2]
l_val = l[1::2]
f1_val = f1[1::2]
mcc_val = mcc[1::2]
a_val = pd.DataFrame({'val_acc':a_val})
l_val = pd.DataFrame({'val_loss':l_val})
f1_val = pd.DataFrame({'val_f1':f1_val})
mcc_val = pd.DataFrame({'val_mcc':mcc_val})
df_acc = pd.concat((a_train,a_val),axis=1)
df_loss = pd.concat((l_train,l_val),axis=1)
df_f1 = pd.concat((f1_train,f1_val),axis=1)
df_mcc = pd.concat((mcc_train,mcc_val),axis=1)
#可視化
fig = plt.figure(figsize=(15,25))
plt.subplots_adjust(wspace=0.4, hspace=0.6)
ax1 = fig.add_subplot(4,1,1)
ax2 = fig.add_subplot(4,1,2)
ax3 = fig.add_subplot(4,1,3)
ax4 = fig.add_subplot(4,1,4)
ax1.grid(True)
ax1.set_xlabel('epoch')
ax1.set_ylabel('Loss')
ax1.plot(df_loss["train_loss"], label="train")
ax1.plot(df_loss["val_loss"], label="val")
ax1.legend()
ax2.grid(True)
ax2.set_xlabel('epoch')
ax2.set_ylabel('ACC')
ax2.plot(df_acc["train_acc"], label="train")
ax2.plot(df_acc["val_acc"], label="val")
ax2.legend()
ax3.grid(True)
ax3.set_xlabel('epoch')
ax3.set_ylabel('F1')
ax3.plot(df_f1["train_f1"], label="train")
ax3.plot(df_f1["val_f1"], label="val")
ax3.legend()
ax4.grid(True)
ax4.set_xlabel('epoch')
ax4.set_ylabel('MCC')
ax4.plot(df_mcc["train_mcc"], label="train")
ax4.plot(df_mcc["val_mcc"], label="val")
ax4.legend()モデルをインスタンス化して、学習を実行します。
# インスタンス化
net = Autoencoder()
# 損失関数の設定
criterion = nn.BCEWithLogitsLoss()
# 最適化手法の選択
optimizer = torch.optim.Adam(net.parameters(), lr=0.0001)
#学習と検証
num_epoch = 100
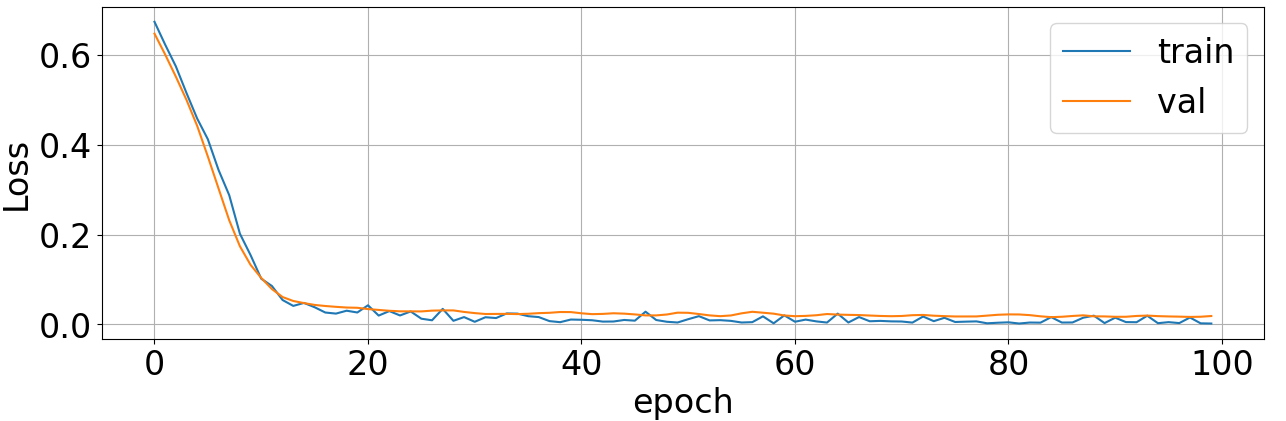
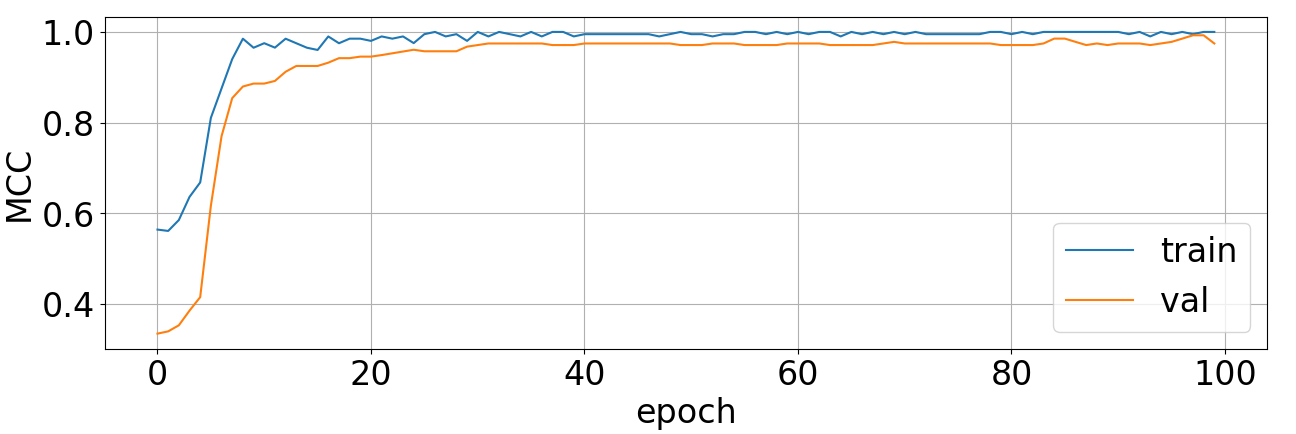
net = train_model(net, criterion, normal_train_loader, anomaly_train_loader, val_loader, optimizer, num_epoch) <損失>
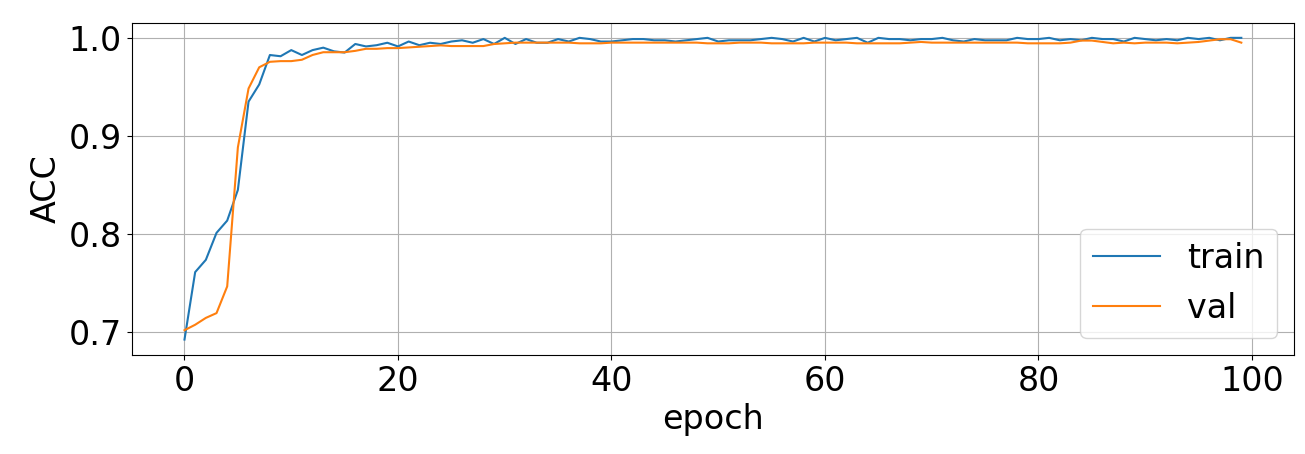
<正解率>
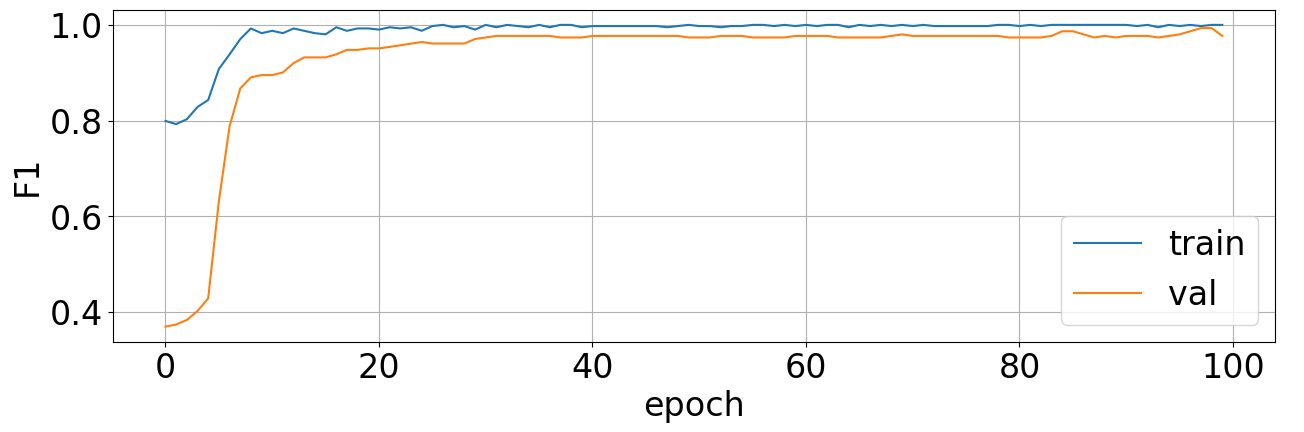
<F1-Score1>
<Matthews Correlation Coefficient>
100epochまでの学習で十分高い精度が得られました。
4.テストデータで精度を確認する
次にテストデータを使ってモデルの精度を確認します。
# 学習時に保存した最適なモデルを呼び出す
# モデル読み込み
best_model = Autoencoder()
best_model.load_state_dict(torch.load('best_model.pth', map_location=torch.device('cpu')), strict=False) #GPU使用可能時はmap_location=torch.device('cpu')を外す
best_model.to("cuda:0" if torch.cuda.is_available() else "cpu")# 正解率を計算する関数
def test_model(test_loader):
device1 = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device2 = torch.device('cpu')
# 勾配計算させないための設定
with torch.no_grad():
# 各バッチごとの結果格納用リスト
accs = []
fls = []
mccs = []
for batch in test_loader:
x, t = batch
x = x.to(device1)
t = t.to(device1)
t = t.view(-1, 1)
y = best_model(x)
feat = best_model.enc(x)
m = nn.Sigmoid()
y_label = torch.round(m(y))
acc = torch.sum(y_label == t) * 1.0 / len(t)
f1 = f1_score(y_label.to(device2), t.to(device2))
mcc = matthews_corrcoef(y_label.to(device2), t.to(device2))
accs.append(acc)
fls.append(f1)
mccs.append(mcc)
print("--"*100)
# テストデータ全体の平均値を算出
avg_acc = torch.tensor(accs).mean()
std_acc = torch.tensor(accs).std()
avg_f1 = mean(fls)
avg_mcc = mean(mccs)
print('Accuracy: {:.1f}%'.format(avg_acc * 100))
print('F1-Score: {:.1f}'.format(avg_f1))
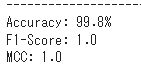
print('MCC: {:.1f}'.format(avg_mcc))# テストデータで精度を確認する
test_model(test_loader)ほぼ100%の正解率となっています。
5.分類寄与度を可視化する
さて、本記事の主題である、「入力データの各時点の分類寄与度」を可視化します。 今回、寄与度の可視化には、テストデータだけでなく全てのデータを使うこととします。 以下が、寄与度可視化のためのコードです。
device1 = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device2 = torch.device('cpu')
normal_inputs = []
normal_labels = []
anomaly_inputs = []
anomaly_labels = []
# 訓練、検証、テスト、全てのデータを使用する
all_batch_size = len(all_dataset)
all_loader = torch.utils.data.DataLoader(all_dataset , batch_size=all_batch_size, shuffle=False)
# 正常データと異常データを分ける
for batch in all_loader:
inputs, labels = batch
inputs = inputs.to(device1)
labels = labels.to(device1)
for i in range(len(labels)):
if labels[i] == 0:
normal_inputs.append(inputs[i].to('cpu').detach().numpy().copy())
normal_labels.append(labels[i].to('cpu').detach().numpy().copy())
else:
anomaly_inputs.append(inputs[i].to('cpu').detach().numpy().copy())
anomaly_labels.append(labels[i].to('cpu').detach().numpy().copy())
# tensor形式へ変換
normal_data = torch.tensor(normal_inputs, dtype=torch.float32)
normal_target = torch.tensor(np.array(normal_labels), dtype=torch.int64)
anomaly_data = torch.tensor(anomaly_inputs, dtype=torch.float32)
anomaly_target = torch.tensor(np.array(anomaly_labels), dtype=torch.int64)
# 目的変数と入力変数をまとめてdatasetに変換
normal_dataset = torch.utils.data.TensorDataset(normal_data, normal_target)
anomaly_dataset = torch.utils.data.TensorDataset(anomaly_data, anomaly_target)
# テストローダー作成
normal_test_loader = torch.utils.data.DataLoader(normal_dataset, batch_size=6402)
anomaly_test_loader = torch.utils.data.DataLoader(anomaly_dataset, batch_size=762)
# 入力に対する損失の勾配を求める
# 正常データ
for batch in normal_test_loader:
inputs, labels = batch
inputs = inputs.to(device1)
labels = labels.to(device1)
labels = labels.view(-1, 1)
# 入力に対する損失の勾配を求める
with torch.set_grad_enabled(True):
inputs = inputs.requires_grad_(True)
outputs = best_model(inputs)
loss = criterion(outputs, labels.to(torch.float32))
# 勾配の計算
grad_x, = torch.autograd.grad(loss, (inputs, ))
# 勾配の平均値に入力データの時点ごとの標準偏差を掛ける
normal_weight = grad_x.mean(dim=0)*torch.std(inputs, dim=0)
# 異常データ
for batch in anomaly_test_loader:
inputs, labels = batch
inputs = inputs.to(device1)
labels = labels.to(device1)
labels = labels.view(-1, 1)
# 入力に対する損失の勾配を求める
with torch.set_grad_enabled(True):
inputs = inputs.requires_grad_(True)
outputs = best_model(inputs)
loss = criterion(outputs, labels.to(torch.float32))
# 勾配の計算
grad_x, = torch.autograd.grad(loss, (inputs, ))
# 勾配の平均値に入力データの時点ごとの標準偏差を掛ける
anomaly_weight = grad_x.mean(dim=0)*torch.std(inputs, dim=0)
fig = plt.figure(figsize=(20,15))
plt.subplots_adjust(wspace=0.4, hspace=0.5)
ax1 = fig.add_subplot(3,1,1)
ax2 = fig.add_subplot(3,1,2)
ax3 = fig.add_subplot(3,1,3)
#正解値の可視化
for i in range(len(normal_labels)):
ax1.plot(normal_inputs[i],color="b",alpha=0.2)
ax1.set_xlabel("Time")
ax1.set_ylabel("Value")
ax1.set_title("normal data")
ax1.grid(True)
for i in range(len(anomaly_labels)):
ax2.plot(anomaly_inputs[i],color="r",alpha=0.2)
ax2.set_xlabel("Time")
ax2.set_ylabel("Value")
ax2.set_title("anomaly data")
ax2.grid(True)
ax3.plot(normal_weight.detach().to(device2).numpy(), c="blue", label="normal")
ax3.plot(anomaly_weight.detach().to(device2).numpy(), c="red", label="anomaly")
ax3.legend(loc="best")
ax3.set_xlabel("Time")
ax3.set_ylabel("Differential value of loss due to input")
ax3.set_title("anomaly data")
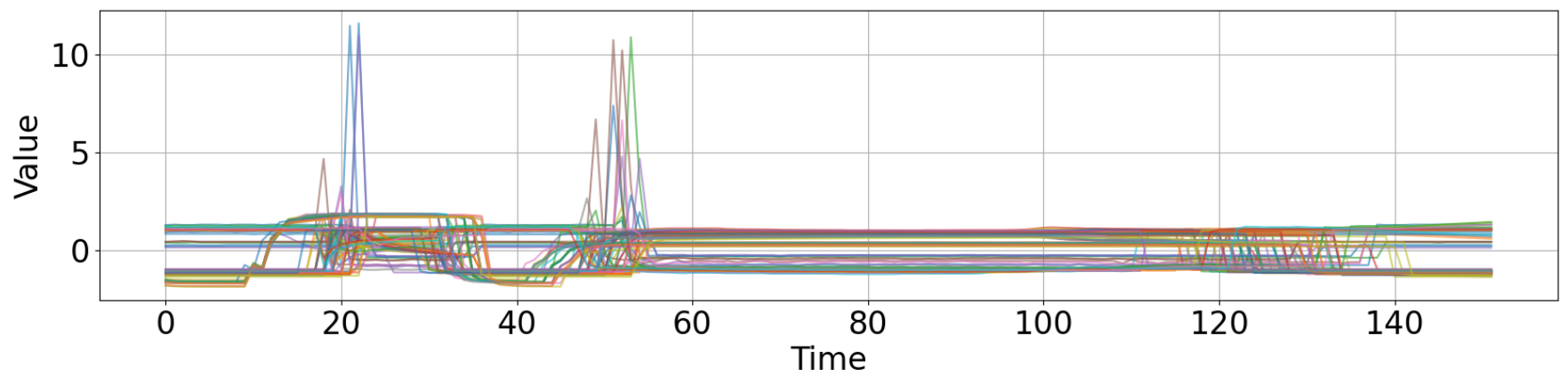
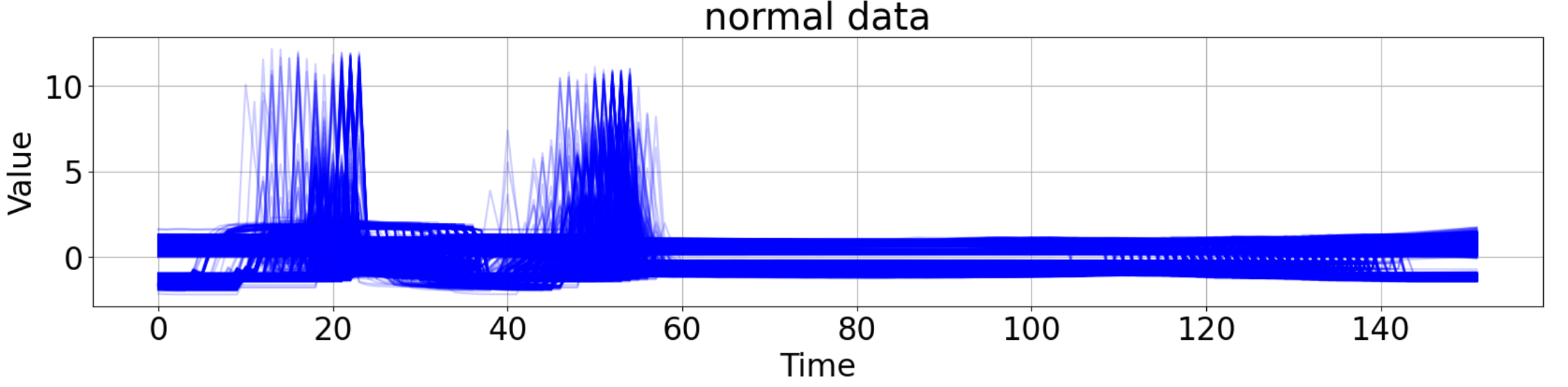
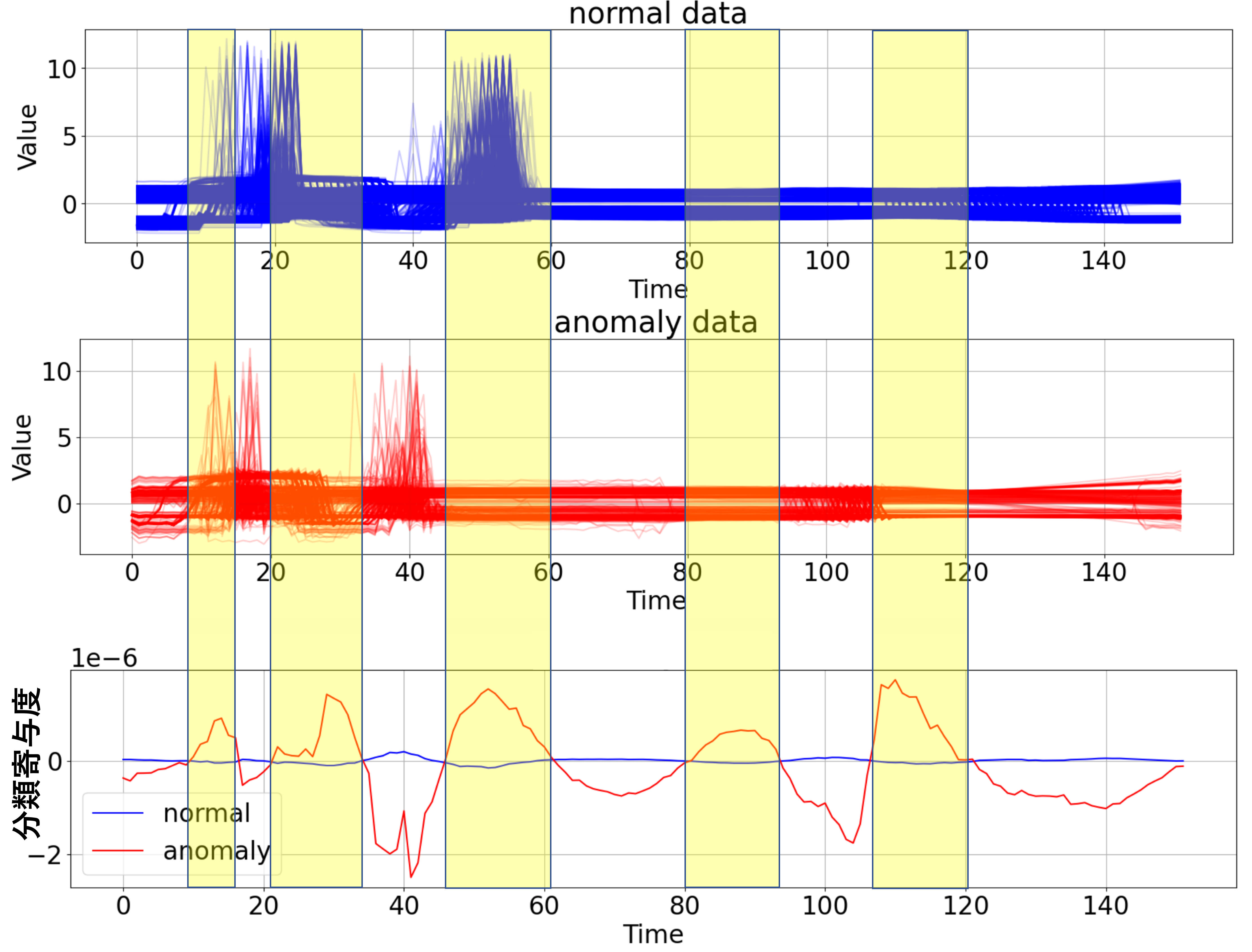
ax3.grid(True)<全ての正常波形>
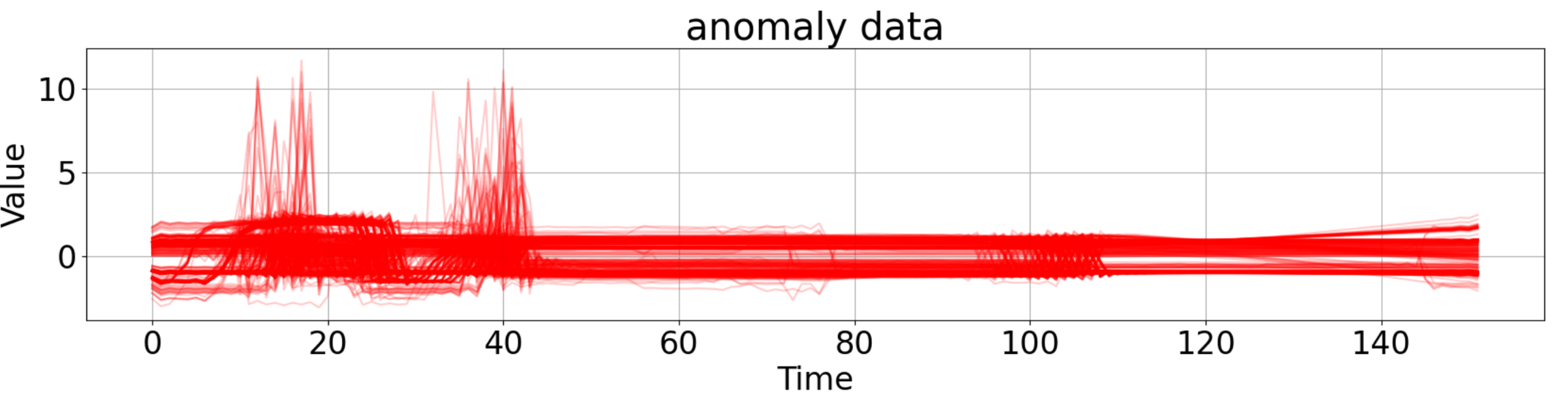
<全ての異常波形>
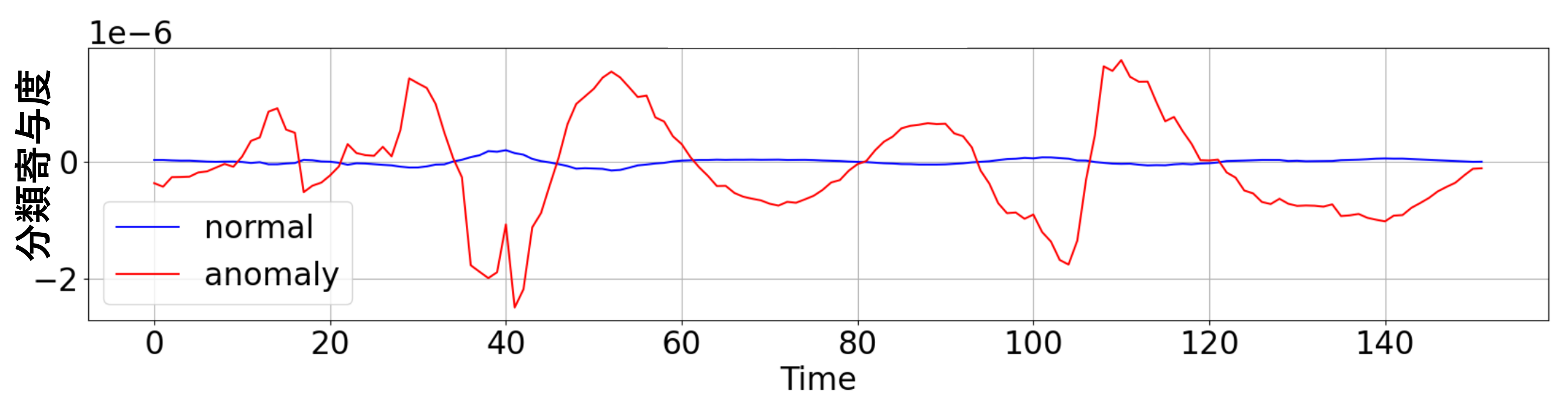
<分類寄与度>
青線:正常波形に対する分類寄与度
赤線:異常波形に対する分類寄与度
正常波形に対する分類寄与度は、どの時点でも0に張り付いています。
これは、正常波形のどの時点の値が変化しても、損失への影響が小さいことを示しています。
一方、異常波形に対する分類寄与度は時点によって大きなバラツキがあることが分かります。
これは、異常波形の各時点の値が変化すると、損失への影響が大きいことを示しています。 これらのことから、CNNモデルは、優先して異常波形から特徴量を抽出し、それを基に正常 or 異常分類していることが推察されます。
分類寄与度を考察する
上図を再掲します。
黄色の領域が、異常データの$i$時点の分類寄与度 > 0の領域です。この領域においては、波形値が減少すると「異常波形」に近づくことを示しています。
一方、色付けしていない領域は、異常データの$i$時点の分類寄与度 < 0の領域です。この領域においては、波形値が増加すると「異常波形」に近づくことを示しています。
ただし、上記は「正常データに対して、異常波形の値が減少すると、、、」という相対比較での結論になります。
正常波形と異常波形と見比べると、$i$時点の分類寄与度 > 0(黄色)となっている領域では確かに、平均的に異常波形の方が値が小さいように思われます(特に、Time = 45~60の領域)。
分類寄与度の活用方法
製造現場での活用方法は2つあると考えています。
1は、システムユーザーである保全員の視点
2は、システム開発者であるデータサイエンティストや機械学習エンジニアの視点 です。
-
- CNNで抽出した特徴そのものを用いて、要因解析や予知保全に活用する
例えば、異常波形は、部品が劣化した際に出力される波形だとしましょう。
この時、部品ごとに異常波形の特徴が異なると仮定します。その上で、これまで実施したとおり、部品ごとに2値分類モデルを作成します。
設備異常が発生した少し前からの波形を分類させて、最も精度良く分類できたモデルを確かめることで、どの備品が壊れたか?を推定できます。
これにより、故障部位特定の時間を短縮することができます。
しかしながら、「分類結果出力だけでは、AIが何を根拠に判断したか分からず不安だし、誤判定時の対策が打てない」との声が現場から上がることがあります。
分類寄与度を分類結果と併せて現場モニターに表示することで、保全員が納得して故障部品を判断することができます。
 マルチンゲールただし、ある程度のエキスパートでないと、分類寄与度を解釈できないと思われます。 昨日入ったばかりの新人には無理だと思われます。。なので、あくまでエキスパート向けの見せ方です。
マルチンゲールただし、ある程度のエキスパートでないと、分類寄与度を解釈できないと思われます。 昨日入ったばかりの新人には無理だと思われます。。なので、あくまでエキスパート向けの見せ方です。
- CNNで抽出した特徴そのものを用いて、要因解析や予知保全に活用する
- CNNで抽出した特徴に着目して、別途特徴量を作成し、要因解析や予知保全に活用する
要因解析や予知保全システムを作る際の大きな関門は「異常波形特有の特徴量」を作成することです。その際、データサイエンティストは、以下の2つの方法を取ることが多いです。特徴量作成の作戦
(A)現場のエキスパートに異常が現れそうな領域、形状をヒアリングする
(B)データサインスを駆使して、特徴量を抽出する
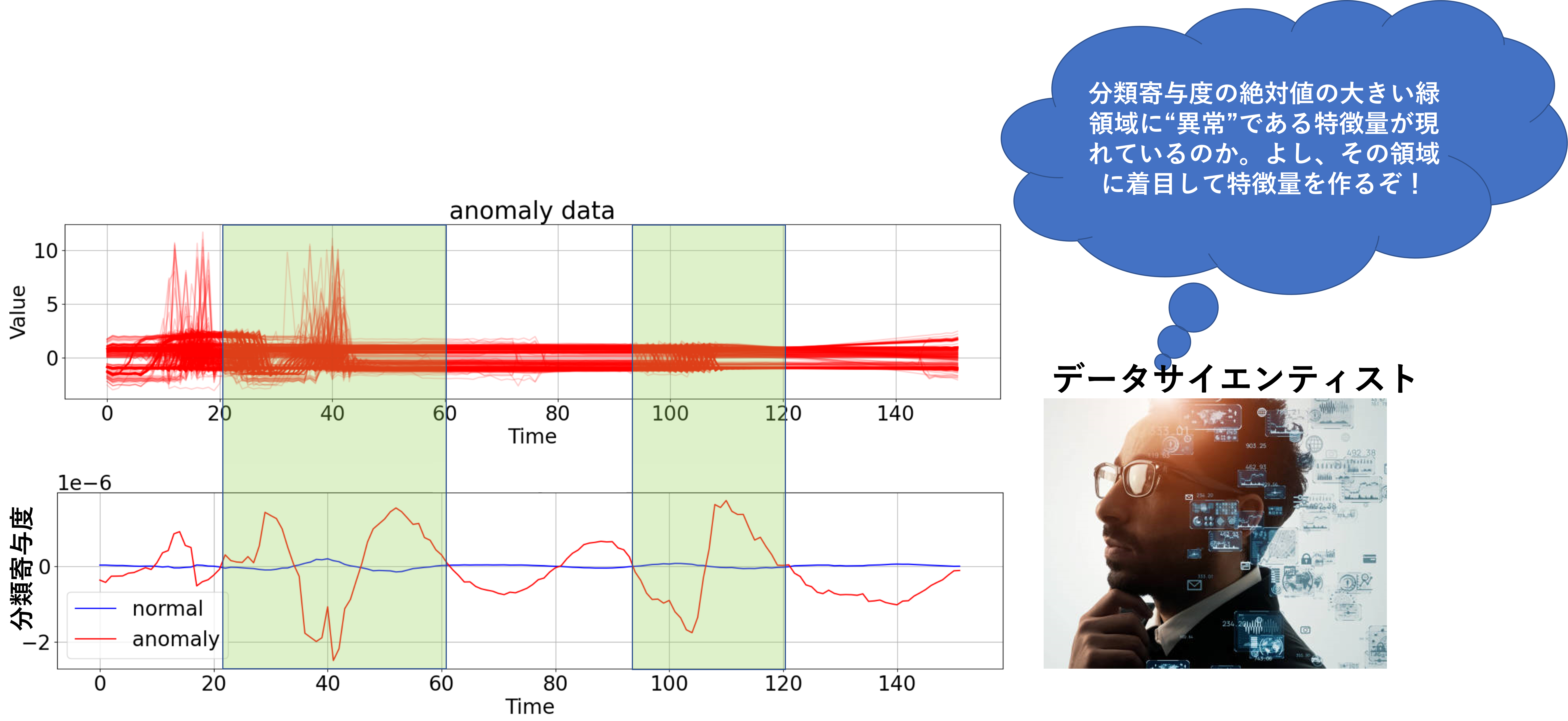
分類寄与度を確かめることで、波形データのどの部位に「正常波形を ”正常たらしめる特徴”、異常波形を”異常たらしめる特徴” が現れているかを知ることができます。
その領域に着目することで有効な特徴量を作成できる可能性があります。
まとめ

ニューラルネットワークは時系列データから特徴量を抽出するための強力なツールです。 データのパターン認識能力は、製造現場のエキスパートのそれを越えていると思います。
しかしながら、業務プロセスへの適用においては、いくつかの注意すべきポイントがあります。
- 時系列データの場合、一般的に前後の大小関係が保たれる標準化を行う (あくまでセオリー的なやり方になります。目的やデータによっては時点毎の標準化が有効な場合もあります。
- 一般的に、製造業で得らるデータは、異常データ数<<正常データ数 です。 そのため、特に工夫せずに学習させると、正常データの分類に偏ったモデルができてしまいます。
訓練データのローダーを作成する際は、1エポック内で異常データ数=正常データ数となるように調整が必要です。 - 製造現場で運用するシステムにおいては、ブラックボックスモデルが受け入れられにくく、結果をユーザーが理解できる様に手助けが必要になります。 その1つの手法として、入力データによる損失の微分があります。