製造工程を管理するために用いられる管理図ですが、生産技術者をやっていた時は、検査装置が自動出力してくれるものを使っていました。
データサイエンティストにキャリアチェンジしてからも、現場のエンジニアと議論する時によく話題に挙がります。(例えば、教師なし学習の文脈で正常データの定義をどするかと言った議論の時など)
そこで、勉強を兼ねて自分で書いてみることにしました。
管理図とは
工程で製造される製品の品質には必ず「バラツキ」があります。このバラツキは以下の2つ分かれます。
- 偶然原因によるバラツキ
管理されている状態でも発生しうるバラツキであり、4M(Man:人、Machine:機械、Method:方法、Material:材料)を標準どおりに行っても生じるやむを得ないバラつきである
- 異常原因によるバラツキ
工程に何か異常が起きていて発生するバラツキ。対策を打たなければいけない
工程を管理するためには、現在起きているバラツキが上記どちらによるものか判断し、異常原因によるバラツキであれば対策を打たなければいけません。管理図はバラツキとそれが偶然か異常か見える化がするために考え出されたツールです。
1本の中心線(CL)とその上下に合理的に決めた管理限界線(UCL , LCL)を作成、特性値が2本の線の間に全てプロットされていれば工程は「管理状態にある」と見なすことができる。
一方、プロットが限界線の外に出た場合、またはプロットの並びにクセが現れた場合には、工程は「管理状態にない」と見なします。
また、管理図には次の2種類があります。
- 解析用管理図
工程解析のための管理図。データを4Mで層別したり、データの分け方(群分け)を変えて管理図を書き、「どこに違いがあるか」、「どれが管理状態にないか」 を調べます。
解析用管理図は、「意思決定のため」、「工程解析のため」、「工程能力調査のため」、「工程の状態を推定するため」に使われます。
- 管理用管理図
解析用管理図を延長して、そこにプロットしながら工程に異常がないか判断するための管理図です。
注意すべきポイントは、管理図は工程の異常を発見するためのツールであり、「不良」を発見するツールではありません。
- 工程異常:不良は発生していないが、不穏な兆候がある状態。製品は良品。
- 工程内不良:規格外れ。製品は不良。
したがって、管理図に規格線(これを超えると不良)は書き込みません。
管理図の種類
管理図には大きく計量値用と計数値用があります。よく使われるのは、計量値用ではないでしょうか。
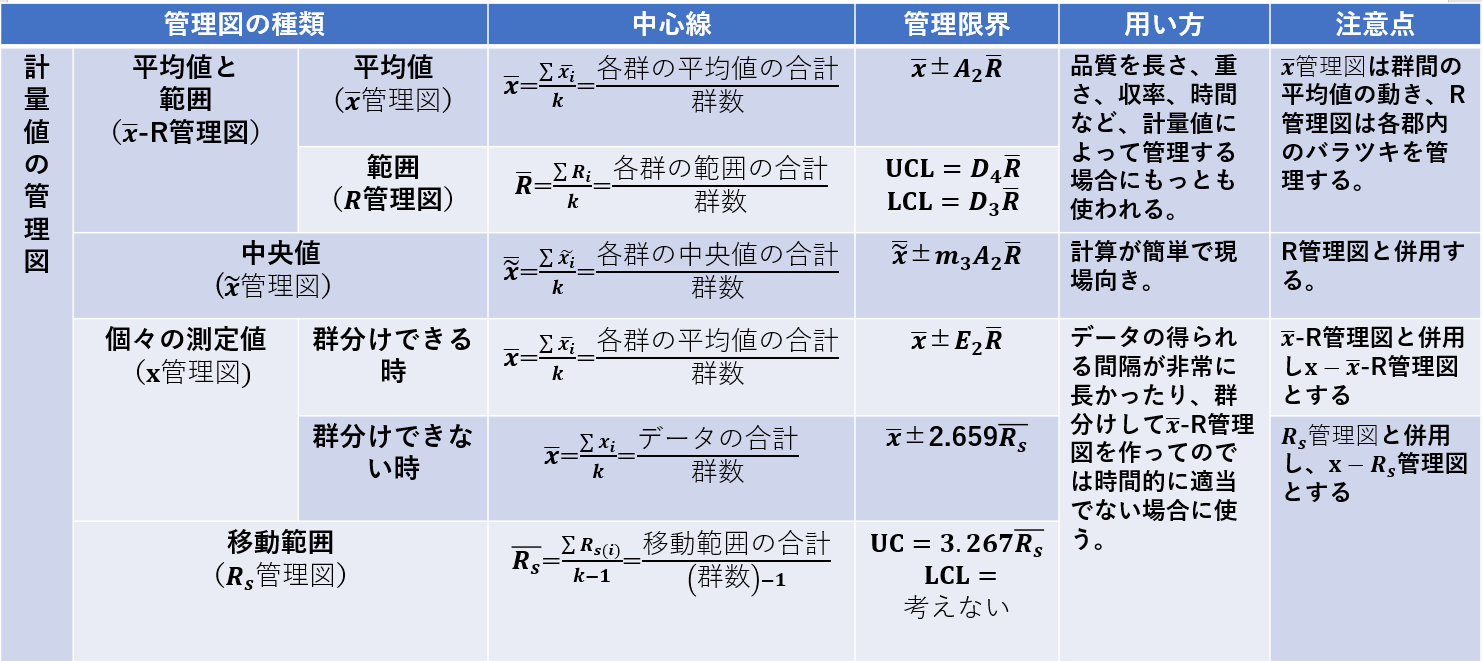
計量値の管理図で管理限界線を決める係数は、過去のデータから試算した±3σ(標準誤差)が使われることが多いですが日本工業規格 JIS Z 9020-2:2016では、以下のように定められています。
管理図作り方
例として、$\bar{x}$管理図の描き方を説明します。
実際は統計S/Wや検査装置付属のS/Wで自動で描けることも多いため作図する機会少ないかも知れません。
[Step1] データを集める
データは履歴がはっきりしている必要があります。
同一製造日、同一材料ロットなどのデータの組を1つの群とします。
⇓
[Step2] 群ごとの平均値$\bar{x}$を計算する
⇓
[Step3] 群ごとの範囲$R$を計算する
⇓
[Step4] 全体の平均を計算する
⇓
[Step5] 範囲の平均値を計算する
⇓
[Step6] $\bar{x}$管理図の管理線を計算する
⇓
[Step7] $R$管理図の管理線を計算する
⇓
[Step8] 管理図を作成する
以下のデータについて、管理図を作成してみます。
表:測定データ
| 製造日(群) | 重量(kg) | 平均値 \(\bar{x}\) |
範囲 \(R\) |
|||
| n1 | n2 | n3 | n4 | |||
| 1 | 77.84 | 78.04 | 78.08 | 77.9 | 77.965 | 0.24 |
| 2 | 78.18 | 78.16 | 78.12 | 78.1 | 78.14 | 0.08 |
| 3 | 78.1 | 78.28 | 78.14 | 78.09 | 78.1525 | 0.19 |
| 4 | 78.16 | 78.12 | 77.98 | 78.09 | 78.0875 | 0.18 |
| 5 | 78.3 | 78.2 | 78.08 | 78.16 | 78.185 | 0.22 |
| 6 | 78.08 | 78 | 77.88 | 78.06 | 78.005 | 0.2 |
| 7 | 78.27 | 78.2 | 78.14 | 78.54 | 78.2875 | 0.4 |
| 8 | 77.97 | 78 | 77.93 | 78.45 | 78.0875 | 0.52 |
| 9 | 78.35 | 78.14 | 78.04 | 77.98 | 78.1275 | 0.37 |
| 10 | 78.1 | 78.65 | 78.1 | 78.18 | 78.2575 | 0.55 |
| 11 | 78.32 | 77.98 | 78.3 | 78.06 | 78.165 | 0.34 |
| 12 | 78.08 | 78.12 | 77.98 | 78.04 | 78.055 | 0.14 |
| 13 | 78.44 | 78.54 | 78.97 | 78.14 | 78.5225 | 0.83 |
| 14 | 78 | 78.09 | 78.18 | 78.05 | 78.08 | 0.18 |
| 15 | 78.16 | 78.44 | 78.09 | 78.08 | 78.1925 | 0.36 |
| 16 | 78.12 | 78.06 | 78.66 | 78.1 | 78.235 | 0.6 |
| 17 | 78.14 | 77.97 | 78.54 | 78.13 | 78.195 | 0.57 |
| 18 | 77.98 | 78.45 | 78.32 | 78.56 | 78.3275 | 0.58 |
| 19 | 78.06 | 78.12 | 78.1 | 78.08 | 78.09 | 0.06 |
| 20 | 78.26 | 78.76 | 78.06 | 78.12 | 78.3 | 0.7 |
| 21 | 78.06 | 78.09 | 78.14 | 78.54 | 78.2075 | 0.48 |
| 22 | 78.02 | 78.12 | 78.12 | 78.65 | 78.2275 | 0.63 |
| 23 | 78.42 | 78.09 | 78.9 | 78.44 | 78.4625 | 0.81 |
| 24 | 78.24 | 78 | 77.76 | 78.14 | 78.035 | 0.48 |
| 25 | 78.1 | 77.99 | 78.08 | 77.98 | 78.0375 | 0.12 |
| 合計 | ー | ー | ー | ー | 1954.428 | 9.83 |
| 平均 | ー | ー | ー | ー | 78.1771 | 0.3932 |
| 標準偏差 | ー | ー | ー | ー | 0.134074 | ー |
[Step4] 、[Step5]の計算は以下のようになります。
$$全体の平均 = 1954.428÷25 = 78.18$$
$$範囲の平均 = 9.83÷25 = 0.39$$
また、管理線は以下のように計算されます。
$$中心線 =\bar{x}=78.18$$
管理限界線は2つの方法で計算してみます。
ポイント ✅ 日本工業規格 JIS Z 9020-2:2016 を使用する場合 下部限界線(LCL)= 全体の平均- \( A_2\)×範囲の平均 = \(78.18-0.729×0.39 = 77.90\) ✅ 全体の平均の標準偏差を使用する場合 上部限界線(UCL)= 全体の平均+ \( 3\)× \( \bar{x} \)の標準偏差= \(78.18+3×0.13 = 78.57\) 下部限界線(LCL)= 全体の平均- \( 3\)× \( \bar{x} \)の標準偏差= \(78.18-3×0.13 = 77.79\) (注)標準偏差は各群の標準偏差ではなく、平均値の標準偏差(=標準誤差)です。
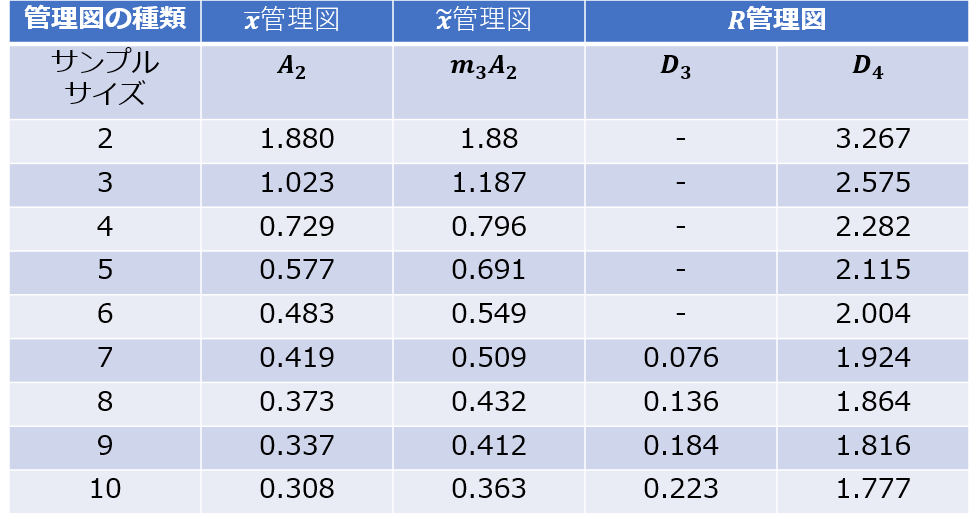
(n=4なので、係数表のサンプルサイズ4の値を使います)
上部限界線(UCL)= 全体の平均+ \( A_2\)×範囲の平均 = \(78.18+0.729×0.39 = 78.46\)
標準偏差を使う場合の方がやや管理幅が広い結果となりました。
上記2つの場合について、管理図を描くと以下のようになります。
管理図作成で注意図べき点は、管理用管理図を作成する際に各群の平均値をプロットするということです。
つまり、上記表でn1~n4の個別の測定値ではなく、平均値の列の値をプロットしてください。
たとえば、n1~n4の値が管理限界線外に発生したとしても、平均値が管理限界線内にあれば、工程異常とは見なしません。
日本工業規格 JIS Z 9020-2:2016 を用いた場合、13日目と23日目に工程異常が発生しましたが、全体の平均の標準偏差を使用する場合を用いたは工程異常は発生していないと判断される結果となりました。
なぜこのような違いが起きたかについて、次章で考えてみたいと思います。
管理限界線はどうやって決まっているか?
上記では、2つの方法で管理限界線決めました。標準偏差を用いた場合は以下の中心極限定理が前提となっています。
中心極限定理 ~和の正規性~
「母集団分布が何であっても、和\( X_1+X_2+X_3+......+X_n\)の確率分布の形は、nが大なるときには、大略正規分布と考えて良い」
統計学入門 東京大学教養学部統計学教室 編 P162 8.2 中心極限定理
$$標本平均\bar{x}を用いて書くと以下のようになります。$$
$$\bar{x} = (X_1+X_2+X_3+......+X_n)/n ~ N(μ , σ^2/n)$$ ・・・(式1)
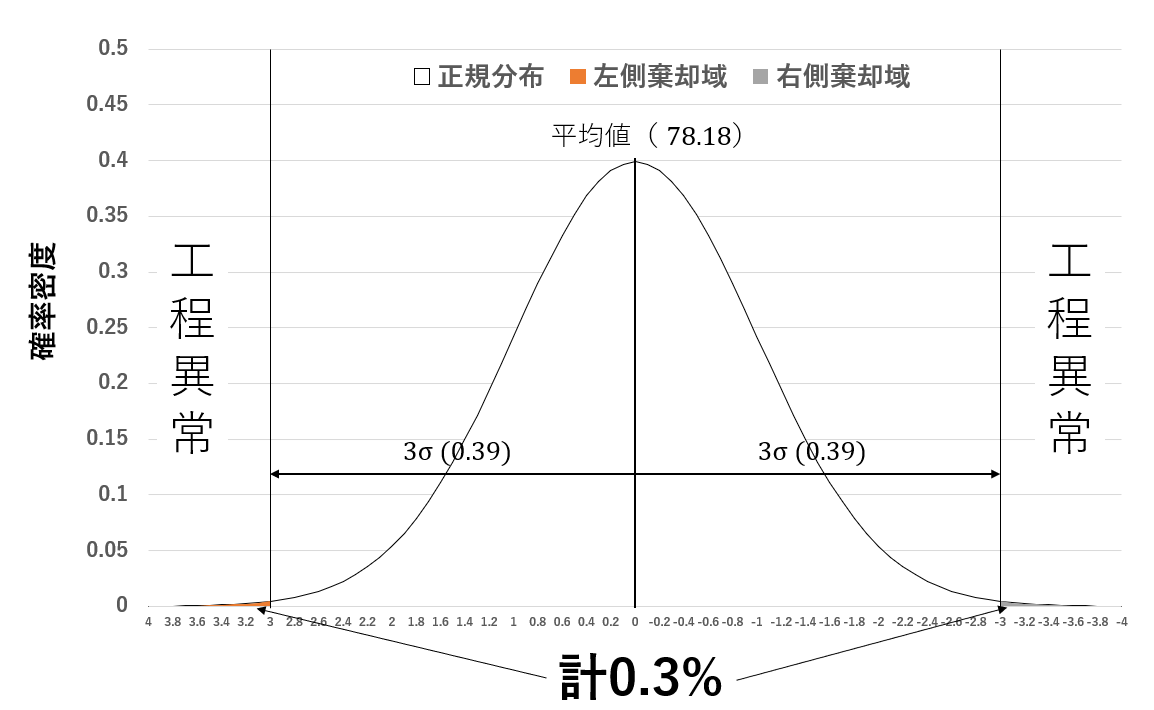
正規分布の場合、以下の図のように全体の平均±3σの 範囲に約99.7%のデータが含まれることになります。この範囲より外側にあるデータは異常原因によるバラツキであると考えます。
(図は前述の表のデータを標準化し、平均0、標準偏差1の正規分布にしています)
ここで、ポイントとなるのは中心極限定理に「nが大なるときには」という文言が入っていることです。
逆に言うとn(サンプルサイズ)が小さい時には(式1)が成り立たないことになります。
つまり、サンプルサイズ(=「表:測定データ」の1つの群の大きさ)が小さい場合には、図3の係数表を用いて管理限界線を決めたほうが妥当と考えられます。
日本工業規格 JIS Z 9020-2:2016 「表2−管理限界線を計算するための係数」には「注a) n>10の群の大きさには用いないのがよい。」と書かれており、n=10がどちらの方法で管理限界線を決めるかの1つの指標になると思われます。
まとめと残る疑問
管理限界線を決める方法は2つあり、サンプルサイズによって使い分けるのが良さそうなことが分かりました。
ポイント ✅ \(サンプルサイズn≦10\) → 日本工業規格 JISの係数表(図3)を使う ✅ \(サンプルサイズn>10\) → 標準誤差を使う
残る疑問点は以下です(今後の宿題、、((´・ω・`))
- 日本工業規格 JISの係数表(日本工業規格 JIS Z 9020-2:2016 「表2−管理限界線を計算するための係数」)の値はどうやって決まっているのか?
- 計数値の管理限界線(図2)は、何故サンプルサイズによらず、標準誤差を用いて試算されるのか?
参考図書
- 統計学入門 (基礎統計学Ⅰ) 東京大学教養学部統計学教室 編 東京大学出版会
- QC七つ道具 (やさしいQC手法演習)新JIS完全対応版 日科技連出版社
https://www.amazon.co.jp/dp/481710418X